“根据《中华人民共和国道路交通安全法》规定：
车辆驾驶员血液酒精浓度在20—80 mg/100ml（不含80）
之间，属于酒后驾车，血液酒精浓度在80mg/100ml
（含80）以上时，属醉酒驾车．”
2009年8月15日晚8时开始某市交警一队在该市
一交通岗前设点对过往的车辆进行抽查，经过两个小时
共查出酒后驾车者60名，图甲是用酒精测试仪对这60
名酒后驾车者血液中酒精浓度进行检测后依所得结果画
出的频率分布直方图．
（1）求这60名酒后驾车者中属醉酒驾车的人数；
（图甲中每组包括左端点，不包括右端点）
（2）统计方法中，同一组数据常用该组区间的中点
值作为代表，图乙的程序框图是对这60名酒后驾车者
血液的酒精浓度做进一步的统计，求出图乙输出的S值，
并说明S的统计意义；（图乙中数据
与
分别表示图 图乙
甲中各组的组中值及频率）
（3）本次行动中，吴、李两位先生都被酒精测试仪测得酒精浓度在70
（含70）以上，但他俩坚称没喝那么多，是测试仪不准，交警大队陈队长决定在被酒精测试仪测得酒精浓度在70（含70）以上的酒后驾车者中随机抽出2人抽血检验，求吴、李两位先生至少有1人被抽中的概率．
设函数F(x )=x2+aln(x+1)
(I)若函数y=f(x)在区间[1,+∞）上是单调递增函数，求实数a的取值范围；
(II)若函数y=f(x)有两个极值点x1,x2且
，求证:
.
椭圆
的左、右焦点分别为F1(-1，0)，F2(1,0)，过F1作与x轴不重合的直线l交椭圆于A,B两点.
(I)若ΔABF2为正三角形，求椭圆的离心率；
(II)若椭圆的离心率满足
,
为坐标原点，求证: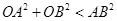
.
如图，在四棱锥P-ABCD中，PA丄平面ABCD,
，
,AD=AB=1,AC和BD交于O点.
(I)求证：平面PBD丄平面PAC.
(II)当点A在平面PBD内的射影G恰好是ΔPBD的重心时，求二面角B-PD-A的余弦值.
为了调査某大学学生在某天上网的时间，随机对lOO名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果：
表l:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(I)从这100名男生中任意选出3人，其中恰有1人上网时间少于60分钟的概率；
(II)完成下面的2X2列联表，并回答能否有90%的把握认为“大学生上网时间与性别有关”？
表3:
•
附：
如图，有两座建筑物AB和CD都在河的对岸（不知 道它们的高度，且不能到达对岸），某人想测量两 座建筑物尖顶A、C之间的距离，但只有卷尺和测 角仪两种工具.若此人在地面上选一条基线EF，用 卷尺测得EF的长度为a，并用测角仪测量了一些角度：
,
，
,
,
请你用文字和公式写出计算A、C之间距离的步骤和结果.