为了调査某大学学生在某天上网的时间,随机对lOO名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:
表l:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(I)从这100名男生中任意选出3人,其中恰有1人上网时间少于60分钟的概率;
(II)完成下面的2X2列联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”?
表3: •
•
附:
已知函数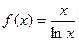 .(Ⅰ)求函数
.(Ⅰ)求函数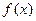 的单调减区间和极值;(Ⅱ)当
的单调减区间和极值;(Ⅱ)当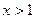 时,若
时,若 恒成立,求实数
恒成立,求实数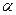 的取值范围.
的取值范围.
有一位于 处的雷达观测站发现其北偏东
处的雷达观测站发现其北偏东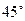 ,相距
,相距 海里的
海里的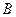 处有一货船正以匀速直线行驶,
处有一货船正以匀速直线行驶,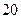 分钟后又测得该船只位于点
分钟后又测得该船只位于点 北偏东
北偏东 (其中
(其中 ,
, )且与点
)且与点 相距
相距 海里的位置
海里的位置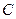 .(Ⅰ)求该船的行驶速度;(Ⅱ)在点
.(Ⅰ)求该船的行驶速度;(Ⅱ)在点 的正南方
的正南方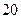 海里
海里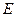 处有一暗礁(不考虑暗礁的面积),如果货船继续前行,它是否有触礁的危险?说明理由
处有一暗礁(不考虑暗礁的面积),如果货船继续前行,它是否有触礁的危险?说明理由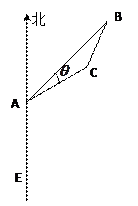

对于数列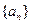 ,规定数列
,规定数列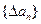 为数列
为数列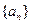 的一阶差分数列,其中
的一阶差分数列,其中 ;一般地,规定
;一般地,规定 为
为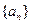 的k阶差分数列,其中
的k阶差分数列,其中 ,且
,且 .(I)已知数列
.(I)已知数列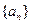 的通项公式
的通项公式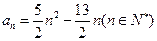 。试证明
。试证明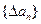 是等差数列;(II)若数列
是等差数列;(II)若数列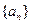 的首项
的首项 ,且满足
,且满足 ,求数列
,求数列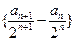 及
及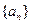 的通项公式;
的通项公式;
如图,菱形ABCD所在平面与矩形ACEF所在平面相互垂直,点M是线段EF的中点。(1)求证:AM // 平面BDE(2)当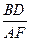 为何值时,平面DEF
为何值时,平面DEF 平面BEF?并证明你的结论。
平面BEF?并证明你的结论。
已知向量 ,
, .(1)当
.(1)当 ,且
,且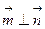 时,求
时,求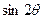 的值;(2)当
的值;(2)当 ,且
,且 ∥
∥ 时,求
时,求 的值.
的值.