如图,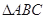 是边长为1的正三角形,
是边长为1的正三角形,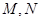 分别是边
分别是边 上的点,
上的点,
段 过
过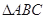 的重心
的重心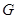 ,设
,设 .
.
(1)当 时,求
时,求 的长;
的长;
(2)分别记 的面积为
的面积为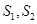 ,试将
,试将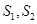 表示为
表示为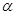 的函数;
的函数;
(3)求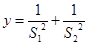 的最大值和最小值。
的最大值和最小值。
(本小题满分12分)
已知函数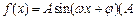 >0,
>0,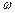 >0,
>0,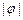 <
<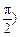 的图象与
的图象与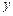
轴的交点为(0,1),它在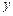 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为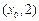 和
和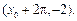
(1)写出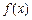 的解析式及
的解析式及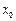 的值
的值 ;
;
(2)若锐角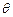 满足
满足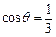 ,求
,求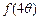 的值.
的值. 
(本小题满分14分)
抛物线D以双曲线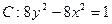 的焦点
的焦点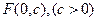 为焦点
为焦点 .
.
(1)求抛物线D的 标准方程;
标准方程;
(2)过直线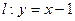 上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐
上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐 标;
标;
(3)在(2)的条件下,若直线PQ交抛物线D于M,N两点,求证:|PM|·|QN|=|QM|·|PN|
(本小题满分13分)
已知数列{an}中,a2=p(p是不等于0的常数),Sn为数列{an}的前n项和,若对任意的正整数n 都有Sn=.
都有Sn=.
(1)证明:数列{an}为等差数列;(2)记 bn=+,求数列{bn}的前n项和Tn;
bn=+,求数列{bn}的前n项和Tn;
(3)记cn=Tn-2n,是否存在正整数N,使得当n>N时,恒有cn∈(,3),若存在,请证明你的结论,并给出一个具体的N值;若不存在,请说明理由.
(本小题满分12分).
已知函数 在
在 上是减函数,在
上是减函数,在 上是增函数,函数
上是增函数,函数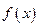 在
在 上有三个零点,且1是其中一个零点.
上有三个零点,且1是其中一个零点.
(1)求 的值; (2)求
的值; (2)求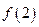 的取值范围;
的取值范围;
(本小题满分12分)如图,一简单组合体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行 四边形,且DC
四边形,且DC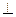 平面ABC.
平面ABC.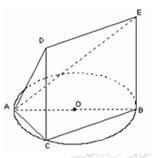
(1)证明:平面ACD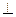 平面
平面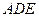 ;
;
(2)若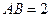 ,
,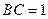 ,
, ,试求该简单组合体的体积V.
,试求该简单组合体的体积V.