(本小题满分12分)
已知函数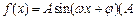 >0,
>0,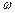 >0,
>0,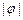 <
<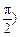 的图象与
的图象与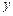
轴的交点为(0,1),它在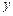 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为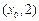 和
和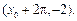
(1)写出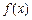 的解析式及
的解析式及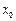 的值
的值 ;
;
(2)若锐角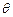 满足
满足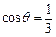 ,求
,求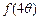 的值.
的值. 
已知单调递增的等比数列 满足:
满足: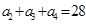 ,且
,且 是
是 ,
,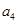 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,
,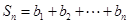 ,求
,求 .
.
在锐角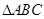 中,
中,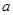 、
、 、
、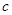 分别为角
分别为角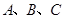 所对的边,且
所对的边,且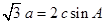 .
.
(Ⅰ)确定角 的大小;
的大小;
(Ⅱ)若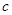 =
= , 且
, 且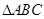 的面积为
的面积为 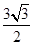
 , 求
, 求 的值.
的值.
已知函数 (
( R,且
R,且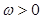 )的部分图象如图所示.
)的部分图象如图所示.
(1) 求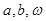 的值;
的值;
(2) 若方程 在
在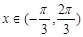 内有两个不同的解,求实数m的取值范围.
内有两个不同的解,求实数m的取值范围.
已知 为锐角
为锐角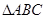 的三个内角,向量
的三个内角,向量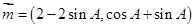 与
与 共线.
共线.
(1)求角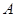 的大小和求角
的大小和求角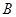 的取值范围;
的取值范围;
(2)讨论函数 的单调性并求其值域.
的单调性并求其值域.
20名学生某次数学考试成绩(单位:分)的频数分布直方图如下: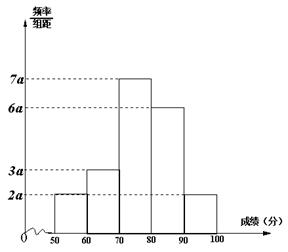
(1)求频率分布直方图中的值;
(2)分别球出成绩落在与中的学生人数;
(3)从成绩在的学生中随机选2人,求此2人的成绩都在中的概率.