某射击运动员为争取获得2010年广州亚运会的参赛资格正在加紧训练.已知在某次训练中他射击了 枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为
枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为 ,设
,设 为本次训练中成绩不低于10环的射击次数,
为本次训练中成绩不低于10环的射击次数, 的数学期望
的数学期望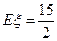 ,方差
,方差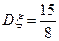 .
.
(1)求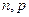 的值;
的值;
(2)训练中教练要求:若有5枪或5枪以上成绩低于10环,则需要补射,求该运动员在本次训练中需要补射的概率.
(结果用分数表示.已知: ,
,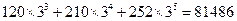 )
)
已知数列 是递增数列,且满足
是递增数列,且满足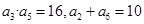 。
。
(1)若 是等差数列,求数列
是等差数列,求数列 的通项公式;
的通项公式;
(2)对于(1)中 ,令
,令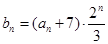 ,求数列
,求数列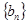 的前
的前 项和
项和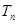 。
。
已知圆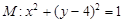 ,直线
,直线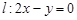 ,点
,点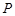 在直线
在直线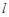 上,过点
上,过点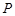 作圆
作圆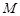 的切线
的切线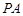 、
、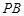 ,切点为
,切点为 、
、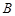 .
.
(Ⅰ)若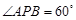 ,求
,求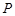 点坐标;
点坐标;
(Ⅱ)若点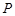 的坐标为
的坐标为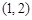 ,过
,过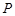 作直线与圆
作直线与圆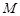 交于
交于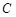 、
、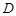 两点,当
两点,当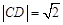 时,求直线
时,求直线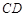 的方程;
的方程;
(III)求证:经过 、
、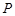 、
、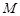 三点的圆与圆
三点的圆与圆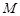 的公共弦必过定点,并求出定点的坐标.
的公共弦必过定点,并求出定点的坐标.
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是底面边长的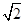 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.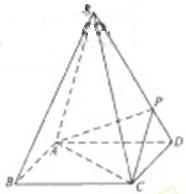
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,则侧棱SC上是否存在一点E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由.
已知圆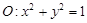 和定点
和定点 ,由圆
,由圆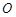 外一点
外一点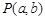 向圆
向圆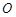 引切线
引切线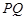 ,切点为
,切点为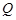 ,且满足
,且满足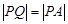 ,
,
(Ⅰ)求实数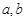 间满足的等量关系;
间满足的等量关系;
(Ⅱ)求线段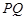 长的最小值.
长的最小值.
如图,在棱长为1的正方体 中.
中.
(Ⅰ)求异面直线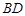 与
与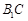 所成的角;
所成的角;
(Ⅱ)求证平面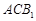 ⊥平面
⊥平面 .
.