设椭圆E的方程为
，点O为坐标原点，点A的坐标为
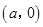，点B的坐标为
，点M在线段AB上，满足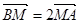
，直线OM的斜率为
.
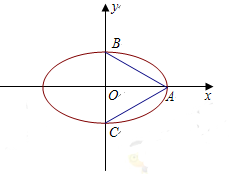
（Ⅰ）求E的离心率e；
（Ⅱ）设点C的坐标为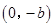
，N为线段AC的中点，点N关于直线AB的对称点的纵坐标为
，求E的方程.
已知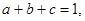
（1）求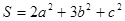
的最小值及取最小值时
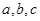的值。
（2）若
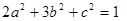，求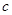
的取值范围。
已知空间4个球,它们的半径分别为2, 2, 3, 3,每个球都与其他三个球外切,另有一个小球与这4个球都外切,则这个小球的半径为（ ）
A． |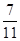
B． |
C． |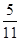
D． |
宇宙深处有一颗美丽的行星，这个行星是一个半径为r（r>0）的球。人们在行星表面建立了与地球表面同样的经纬度系统。已知行星表面上的A点落在北纬60°，东经30°；B点落在东经30°的赤道上；C点落在北纬60°，东经90°。在赤道上有点P满足PB两点间的球面距离等于AB两点间的球面距离。
（1）求AC两点间的球面距离；
（2）求P点的经度；
（3）求AP两点间的球面距离。
设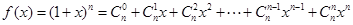
（
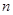是正整数），利用赋值法解决下列问题：
（1）求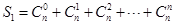
；
（2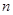）为偶数时，求
；
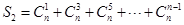（3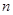）是3的倍数时，求
。
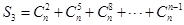已知：对于任意的多项式
与任意复数z，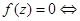
整除。利用上述定理解决下列问题：
在复数范围内分解因式：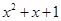
；
求所有满足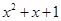整除
的正整数n构成的集合A。