18．（本小题满分14分）
如图5，四边形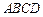
是圆柱
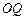的轴截面，点
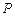在圆柱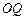的底面圆周上，
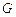是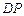
的中点，圆柱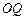的底面圆的半径
，侧面积为
，
．
（1）求证：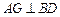
；
（2）求二面角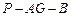
的平面角的余弦值．
如图，在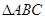
中，
，点
在
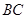边上，且
（1）求
（2）求
的长．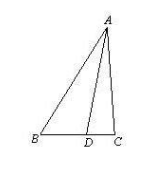
已知函数
（1）解不等式
；
（2）若不等式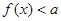
的解集为空集，求实数
的取值范围．
已知函数
的减区间是（-2，2）
（1）试求m,n的值；
（2）求过点
且与曲线
相切的切线方程；
（3）过点A(1,t)，是否存在与曲线相切的3条切线，若存在，求实数t的取值范围；若不存在，请说明理由．
已知函数
，
．
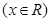(1)求
在点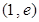
处的切线方程；
(2)证明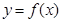: 曲线
与曲线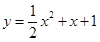
有唯一公共点；
(3)设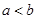
，比较
与
的大小, 并说明理由.
在平面直角坐标系xOy中，已知椭圆C1：
＝1(a>b>0)的左焦点为F1(－1，0)，且点P(0，1)在C1上．
(1)求椭圆C1的方程；
(2)设直线l同时与椭圆C1和抛物线C2：y2＝4x相切，求直线l的方程．