某地区举行环保知识大赛,比赛分初赛和决赛两部分,初赛采用选用选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题直接进入决赛,答错3次者则被淘汰,已知选手甲连续两次
答错的概率为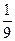 (已知甲回答每个问题的正确率相同,且相互之间没有影响)
(已知甲回答每个问题的正确率相同,且相互之间没有影响)
(I)求甲选手回答一个问题的正确率;
(II)求选手甲进入决赛的概率;
(III)设选手甲在初赛中的答题的个数为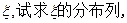 并求出
并求出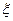 的数学期望。
的数学期望。
已知函数f(x)=2 sin xcos x+2cos2x+m在区间
sin xcos x+2cos2x+m在区间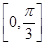 上的最大值为2.
上的最大值为2.
(1)求常数m的值;
(2)在△ABC中,内角A,B,C所对的边分别为a,b,c,若f(A)=1,sin B=3sin C,△ABC的面积为 ,求边长a.
,求边长a.
等比数列{cn}满足cn+1+cn=10·4n-1(n∈N*),数列{an}的前n项和为Sn,且an=log2cn.
(1)求an,Sn;
(2)数列{bn}满足bn=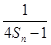 ,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
数列{an}中,a1=3,an+1=an+cn(c是常数,n=1,2,3,…),且a1,a2,a3成公比不为1的等比数列.
(1)求c的值;
(2)求数列{an}的通项公式.
在数列{an}和等比数列{bn}中,a1=0,a3=2,bn=2an+1(n∈N*).
(1)求数列{bn}及{an}的通项公式;
(2)若cn=an·bn,求数列{cn}的前n项和Sn.
已知各项均为正数的等比数列{an}的首项a1=2,Sn为其前n项和,若5S1,S3,3S2成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log2an,cn=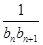 ,记数列{cn}的前n项和Tn.若对n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围.
,记数列{cn}的前n项和Tn.若对n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围.