国家助学贷款是由财政贴息的信用贷款，旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2010届毕业生凌霄在本科期间共申请了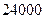
元助学贷款，并承诺在毕业后
年内（按
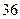个月计）全部还清.
签约的单位提供的工资标准为第一年内每月
元，第
个月开始，每月工资比前一个月增加
直到
元.凌霄同学计划前
个月每个月还款额为
，第个月开始，每月还款额比前一月多
元.
（Ⅰ）若凌霄恰好在第36个月（即毕业后三年）还清贷款，求的值；
（Ⅱ）当
时，凌霄同学将在第几个月还清最后一笔贷款？他当月工资的余额是否能满足每月
元的基本生活费？
（参考数据：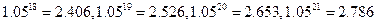
）
如图，ABCD是边长为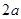
的正方形，ABEF是矩形，且二面角C
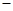AB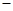F是直二面角，
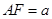，G是EF的中点，
（1）求GB与平面AGC所成角的正弦值.
（2）求二面角B—AC—G的余弦值.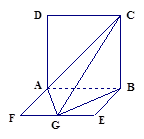
已知
，讨论方程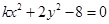
所表示的圆锥曲线类型，并求其焦点坐标
某班同学利用国庆节进行社会实践，对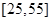
岁的人群随机抽取
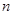人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：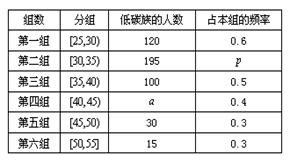
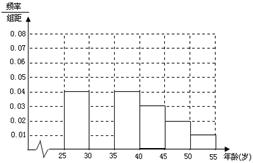
（Ⅰ）补全频率分布直方图并求、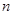
、
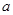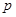的值；
（Ⅱ）试由各年龄段人数频率分布直方图估计这随机抽取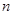人的平均年龄。
设p：实数x满足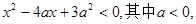
q：实数x满足
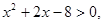且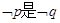
的必要不充分条件，求a的取值范围。
从3个黑球和2个白球的袋中不放回的取出2个球，每次取球都是等可能的
（1）求所取2个球中全是黑球的概率；
（2）求所取2个球中恰有1个白球的概率