从3个黑球和2个白球的袋中不放回的取出2个球,每次取球都是等可能的
(1)求所取2个球中全是黑球的概率;
(2)求所取2个球中恰有1个白球的概率
(本小题满分10)选修4-5:不等式选讲
已知函数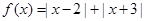 的最小值为
的最小值为 .
.
(Ⅰ)求 ;
;
(Ⅱ)当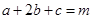 时,求
时,求 的最小值.
的最小值.
(本小题满分10)选修4-4:坐标系与参数方程
在直角坐标系 中,已知曲线
中,已知曲线 的参数方程是
的参数方程是 (
( 为参数).在极坐标系(与直角坐标系
为参数).在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的极坐标方程是
的极坐标方程是 .
.
(Ⅰ)求曲线 的普通方程和直线
的普通方程和直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)点 是曲线
是曲线 上的动点,求点
上的动点,求点 到直线
到直线 距离的最小值.
距离的最小值.
(本小题满分10)选修4—1:几何证明选讲
如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.
(1)求证:圆心O在直线AD上;
(2)求证:点C是线段GD的中点.
(本小题满分12分)已知函数 为自然对数的底数)
为自然对数的底数)
(1)求函数 的最小值;
的最小值;
(2)若 ≥0对任意的x∈R恒成立,求实数a的值;
≥0对任意的x∈R恒成立,求实数a的值;
(3)在(2)的条件下,证明:
(本小题满分12分)已知抛物线 ,圆
,圆 ,过点
,过点 作直线
作直线 ,自上而下依次与上述两曲线交于点
,自上而下依次与上述两曲线交于点 (如图所示),
(如图所示), .
.
(Ⅰ)求 ;
;
(Ⅱ)作 关于
关于 轴的对称点
轴的对称点 ,求证:
,求证:  三点共线;
三点共线;
(Ⅲ)作 关于
关于 轴的对称点
轴的对称点 ,求
,求 到直线
到直线 的距离的最大值.
的距离的最大值.