(本小题满分12分)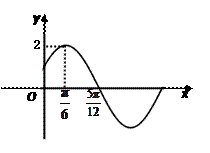
已知函数 的部分图象如图所示.
的部分图象如图所示.
(1)求函数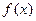 的解析式;
的解析式;
(2)令 ,判断函数
,判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(本小题满分10分)
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21 人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(Ⅰ)根据以上数据建立一个2×2的列联表;
(Ⅱ)判断性别与休闲方式是否有关系.
(本小题13分)
|
已知函数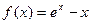 (
( 为自然对数的底数)
为自然对数的底数)
 的最小值;
的最小值;
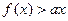 的解集为P,且
的解集为P,且 ,求实数a的取值范围。
,求实数a的取值范围。
(本小题10分)
已知数列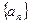 中,
中,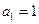
 。
。
(Ⅰ)求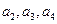 的值;
的值;
(Ⅱ)猜想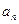 的通项公式,并用数学归纳法给予证明。
的通项公式,并用数学归纳法给予证明。
(本小题10分)
在边长为60cm的正方形铁皮的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
(本小题9分)
已知复数 ,当实数
,当实数 为何值时,
为何值时,
(1) 为实数;
为实数;
(2) 为虚数;
为虚数;
(3) 为
为 纯虚数.
纯虚数.