(本小题满分12分)
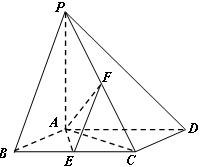
已知四棱锥 的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱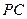 上的动点.
上的动点.
(1)求证:
(2)若五点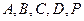 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
 |
|||
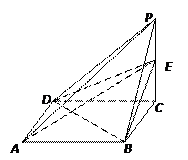 |
|||
(本小题满分12分)
桌面上有三颗均匀的骰子(6个面上分别标有数字1,2,3,4,5,6)。重复下面的操作,直到桌面上没有骰子:将骰子全部抛掷,然后去掉那些朝上点数为奇数的骰子。记操作三次之内(含三次)去掉的骰子的颗数为X.
(Ⅰ)求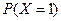 ;
;
(Ⅱ)求X的分布列及期望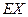
 .
.
(本小题满分12分)
已知函数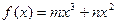 (
(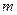 ,
,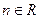 ,
,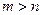 且
且 )的图象在
)的图象在 处的切线与
处的切线与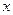 轴平行.
轴平行.
(1) 试确定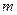 、
、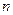 的符号;
的符号;
(2) 若函数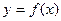 在区间
在区间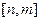 上有最大值为
上有最大值为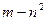 ,试求
,试求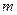 的值.
的值.
(本小题满分12分)
设椭圆C1: 的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2: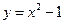 与y轴的交点为B,且经过F1,F2点。
与y轴的交点为B,且经过F1,F2点。
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设M(0, ),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求
),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求 面积的最大值。
面积的最大值。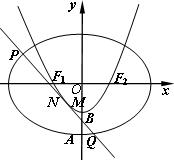
(本小题满分12分)
已知数列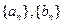 满足
满足 ,
,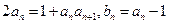 ,设数列
,设数列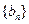 的前n项和为
的前n项和为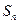 ,令
,令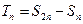 。
。
(Ⅰ)求数列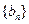 的通项公式;(Ⅱ)判断
的通项公式;(Ⅱ)判断 的大小,并说明理由。
的大小,并说明理由。
(本小题满分12分)
如图,已知四棱锥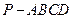 ,底面
,底面 为菱形,
为菱形, 平面
平面 ,
,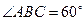 ,
, 分别是
分别是 的中点.
的中点.
(Ⅰ)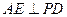 判定AE与PD是否垂直,并说明理由
判定AE与PD是否垂直,并说明理由
(Ⅱ)若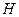 为
为 上的动点,
上的动点,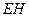 与平面
与平面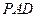 所成最大角的正切值为
所成最大角的正切值为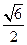 ,求二面角
,求二面角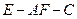 的余弦值。
的余弦值。