(本小题满分12分)
如图,已知四棱锥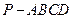 ,底面
,底面 为菱形,
为菱形, 平面
平面 ,
,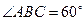 ,
, 分别是
分别是 的中点.
的中点.
(Ⅰ)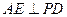 判定AE与PD是否垂直,并说明理由
判定AE与PD是否垂直,并说明理由
(Ⅱ)若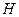 为
为 上的动点,
上的动点,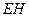 与平面
与平面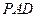 所成最大角的正切值为
所成最大角的正切值为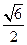 ,求二面角
,求二面角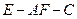 的余弦值。
的余弦值。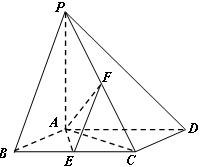
求曲线y=sinx与直线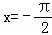 ,
, ,y=0所围成的平面图形的面积.
,y=0所围成的平面图形的面积.
设命题p:(4x﹣3)2≤1;命题q:x2﹣(2a+1)x+a(a+1)≤0,若¬p是¬q的必要不充分条件,求实数a的取值范围.
已知P={x|x2﹣8x﹣20≤0},S={x|1﹣m≤x≤1+m}
(1)是否存在实数m,使x∈P是x∈S的充要条件,若存在,求出m的取值范围;
(2)是否存在实数m,使x∈P是x∈S的必要条件,若存在,求出m的取值范围.
已知数列{an}的前n项和Sn= n2+
n2+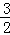 n.
n.
(1)求数列{an}的通项公式;
(2)记Tn=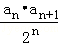 ,若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围.
,若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围.
某工厂引入一条生产线,投人资金250万元,每生产x千件,需另投入成本w(x),当年产量不足80干件时,w(x)= x2+10x(万元),当年产量不小于80千件时,w(x)=51x+
x2+10x(万元),当年产量不小于80千件时,w(x)=51x+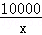 ﹣1450(万元),当每件商品售价为500元时,该厂产品全部售完.
﹣1450(万元),当每件商品售价为500元时,该厂产品全部售完.
(Ⅰ)写出年利润L(x)(万元)与年产量x(千件)的函数关系式;
(Ⅱ)年产量为多少千件时该厂的利润最大.