.如图5,四棱锥 中,底面
中,底面 为矩形,
为矩形,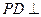 底面
底面 ,
, ,
, 分别为
分别为 的中点
的中点
(1)求证: 面
面 ;
;
(2)若 ,求
,求 与面
与面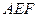 所成角的余弦值
所成角的余弦值
在平面直角坐标系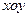 中,设点
中,设点 (1,0),直线
(1,0),直线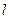 :
: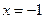 ,点
,点 在直线
在直线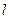 上移动,
上移动, 是线段
是线段 与
与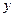 轴的交点,
轴的交点, 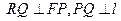 .
.
(Ⅰ)求动点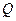 的轨迹的方程;
的轨迹的方程;
(Ⅱ) 记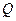 的轨迹的方程为
的轨迹的方程为 ,过点
,过点 作两条互相垂直的曲线
作两条互相垂直的曲线 的弦
的弦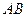 、
、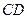 ,设
,设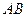 、
、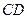 的中点分别为
的中点分别为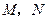 .求证:直线
.求证:直线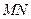 必过定点
必过定点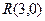 .
.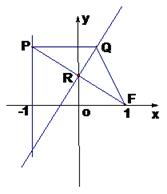
已知椭圆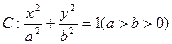 的离心率为
的离心率为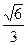 ,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且
,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且 ,定点A(-4,0).
,定点A(-4,0).
(1)求证:当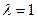 时.,
时.,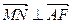 ;
;
(2)若当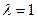 时有
时有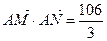 ,求椭圆C的方程;
,求椭圆C的方程;
(3)在(2)的条件下,当M、N两点在椭圆C运动时,当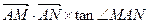 的值为6
的值为6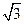 时, 求出直线MN的方程.
时, 求出直线MN的方程.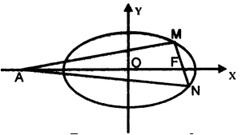
设直线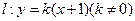 与椭圆
与椭圆 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
(1)证明: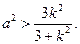 ;
;
(2)若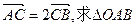 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
设动点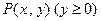 到定点
到定点
 的距离比它到
的距离比它到 轴的距离大1,记点
轴的距离大1,记点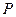 的轨迹为曲线
的轨迹为曲线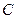 .
.
(1)求点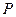 的轨迹方程;
的轨迹方程;
(2)设圆 过
过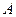
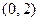 ,且圆心
,且圆心 在曲线
在曲线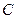 上,
上,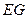 是圆
是圆 在
在 轴上截得的弦,试探究当
轴上截得的弦,试探究当 运动时,弦长
运动时,弦长 是否为定值?为什么?
是否为定值?为什么?
已知椭圆C: 的左、右焦点为F1、F2,离心率为e. 直线
的左、右焦点为F1、F2,离心率为e. 直线 与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
(Ⅰ)证明: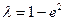 ;
;
(Ⅱ)若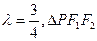 的周长为6;写出椭圆C的方程.
的周长为6;写出椭圆C的方程.