2008年奥运会的一套吉祥物有五个，分别命名:“贝贝”、
“晶晶”、“欢欢”、“迎迎”和“妮妮”，称“奥运福娃”。甲、乙两位小学生各有一套吉祥物，现以投掷一个骰子的方式进行游戏，规则如下：当出现向上的点数是奇数时，甲将赢得乙一个福娃；否则乙赢得甲一个福娃。现规定掷骰子的总次数达9次时，或在此
前某学生已赢得所有福娃时游戏终止，记游戏终止时投掷骰子的总次数为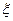
．
（1）求掷骰子的次数为7的概率；
（2）求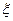的分布列及数学期望E．
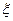已知集合A＝{x∈R|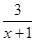
≥1}，集合B＝{x∈R|y＝
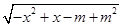}，若A∪B＝A，求实数m的取值范围．
设函数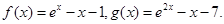
解不等式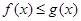
；
事实上：对于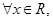
有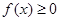
成立，当且仅当
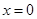时取等号.由此结论证明:
.
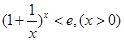如图，AB是圆的直径，PA垂直圆所在的平面，C是圆周上的一点．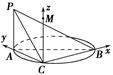
（1）求证：平面PAC⊥平面PBC；(6分)
（2）若AB＝2，AC＝1，PA＝1，求二面角CPBA的余弦值．
已知函数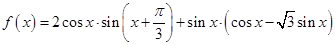
（1）求函数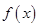
的最小正周期和单调递减区间；；
（2）在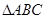
中，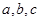
分别是角A、B、C的对边，若
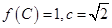,求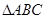面积的最大值．
为了估计某校的某次数学考试情况，现从该校参加考试的600名学生中随机抽出60名学生，其成绩（百分制）均在
上，将这些成绩分成六段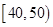
，
，…
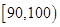，后得到如图所示部分频率分布直方图．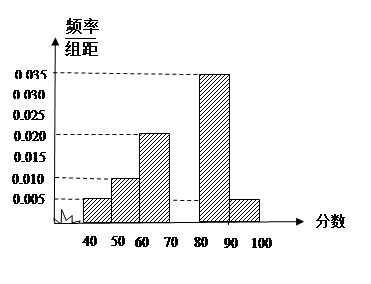
（1）求抽出的60名学生中分数在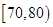
内的人数；
（2）若规定成绩不小于85分为优秀，则根据频率分布直方图，估计该校优秀人数．