(本小题满分12分)如图,在正三棱柱 中,
中, 分别是
分别是 的中点,
的中点, .
.
(Ⅰ)在棱 上是否存在点
上是否存在点 使
使 ?如果存在,试确定它的位置;如果不存在,请说明理由;
?如果存在,试确定它的位置;如果不存在,请说明理由;
(Ⅱ)求截面 与底面
与底面 所成锐二面角的正切值;
所成锐二面角的正切值;
(Ⅲ)求点 到截面
到截面 的距离.
的距离.
(本小题满分10分)若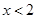 ,求:函数
,求:函数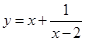 的最大值.
的最大值.
(本小题满分14分)
已知函数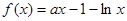
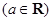 .
.
(1)讨论函数 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数 在
在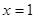 处取得极值,对
处取得极值,对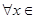
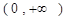 ,
,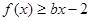 恒成立,求实数
恒成立,求实数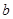 的取值范围;
的取值范围;
(3)当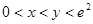 且
且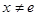 时,试比较
时,试比较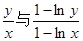 的大小.
的大小.
(本小题满分14分)
在平面直角坐标系内已知两点A(-1,0)、B(1,0),若将动点P(x,y)的横坐标保持不变,纵坐标扩大到原来的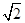 倍后得到点Q(x,
倍后得到点Q(x,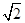 y),且满足
y),且满足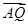 ·
·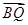 ="1."
="1."
(1)求动点P所在曲线C的方程;
(2)过点B作斜率为-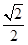 的直线L交曲线C于M、N两点,且
的直线L交曲线C于M、N两点,且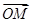 +
+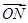 +
+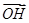 =
=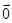 ,试求△MNH的面积.
,试求△MNH的面积.
(本小题满分14分)
已知数列 中,
中,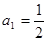 ,
,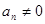 ,
, 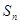 为该数列的前
为该数列的前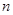 项和,且
项和,且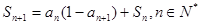 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若不等式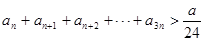 对一切正整数
对一切正整数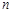 都成立,求正整数
都成立,求正整数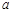 的最大值,并证明结论.
的最大值,并证明结论.
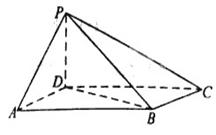
(本小题共14分)如图,四棱锥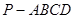 中,底面
中,底面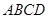 为平行四边形,
为平行四边形,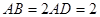 ,
,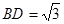 ,
, ⊥底面
⊥底面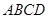 .
.
(1)证明:平面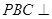 平面
平面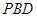 ;
;
(2)若二面角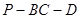 为
为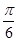 ,求
,求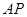 与平面
与平面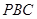 所成角的正弦值。
所成角的正弦值。