已知数列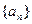
的通项公式是
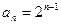，数列
是等差数列，令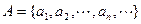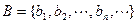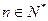集合
，
，
．将集合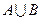
中的元素按从小到大的顺序排列构成的数列记为
．
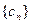（1）若
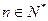，，求数列的通项公式；
（2）若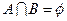
，数列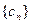的前5项成等比数列，且
，
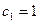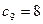，求满足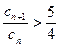
的正整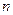数
的个数．
如图，在四棱锥P-ABCD中，ABCD为平行四边形，
平面PAB,
,
.M为PB的中点.
（1）求证：PD//平面AMC；
（2）求锐二面角B-AC-M的余弦值.
某班共有学生40人，将以此数学考试成绩（单位：分）绘制成频率分布直方图，如图所示.
（1）请根据图中所给的数据，求a的值；
（2）从成绩在[50,70)内的学生中随机选3名学生，求这3名学生的成绩都在[60,70)内的概率；
（3）为了了解学生这次考试的失分情况，从成绩在[50,70)内的学生中随机选取3人的成绩进行分析，用X表示所选学生成绩在[60,70)内的人数，求X的分布列和数学期望.
已知函数
的部分图像如图所示.
（1）求函数f(x)的解析式，并写出f(x)的单调减区间；
（2）
的内角分别是A,B,C.若f(A)=1,
,求sinC的值.
在数列
中，
.从数列中选出
项并按原顺序组成的新数列记为
，并称为数列的
项子列.例如数列
、
、
、
为的一个
项子列.
（1）试写出数列的一个
项子列，并使其为等比数列；
（2）如果为数列的一个
项子列，且为等差数列，证明：的公差
满足
；
（3）如果
为数列的一个
项子列，且为等比数列，证明：
.
已知椭圆
的焦距为
，过右焦点和短轴一个端点的直线的斜率为
，
为坐标原点.
（1）求椭圆
的方程.
（2）设斜率为
的直线
与相交于
、
两点，记
面积的最大值为
，证明：
.