在数列 中,
中, .从数列
.从数列 中选出
中选出 项并按原顺序组成的新数列记为
项并按原顺序组成的新数列记为 ,并称
,并称 为数列
为数列 的
的 项子列.例如数列
项子列.例如数列 、
、 、
、 、
、 为
为 的一个
的一个 项子列.
项子列.
(1)试写出数列 的一个
的一个 项子列,并使其为等比数列;
项子列,并使其为等比数列;
(2)如果 为数列
为数列 的一个
的一个 项子列,且
项子列,且 为等差数列,证明:
为等差数列,证明: 的公差
的公差 满足
满足 ;
;
(3)如果 为数列
为数列 的一个
的一个 项子列,且
项子列,且 为等比数列,证明:
为等比数列,证明: .
.
化简、求值
(1) 化简
化简
(2) 已知 均为锐角,
均为锐角, ,求
,求 的值
的值
设数列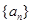 的前
的前 项和为
项和为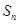 ,
, ,数列
,数列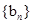 的通项公式为
的通项公式为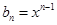 .
.
(1)求数列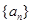 的通项公式;
的通项公式;
(2)设 ,数列
,数列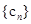 的前
的前 项和为
项和为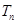 ,
,
①求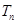 ;
;
②若 ,求数列
,求数列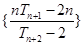 的最小项的值.
的最小项的值.
已知集合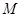 是满足下列性质的函数
是满足下列性质的函数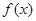 的全体:在定义域
的全体:在定义域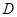 内存在
内存在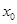 ,使得
,使得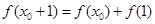 成立.
成立.
(1)函数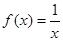 是否属于集合
是否属于集合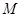 ?说明理由;
?说明理由;
(2)若函数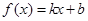 属于集合
属于集合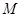 ,试求实数
,试求实数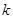 和
和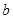 的取值范围;
的取值范围;
(3)设函数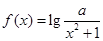 属于集合
属于集合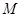 ,求实数
,求实数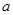 的取值范围.
的取值范围.
某企业11年底投入100万元,购入一套污水处理设备,该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费是2万元,由于设备老化,以后每年的维护费用都比上一年增加2万元.
⑴求该企业使用设备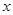 年的年平均污水处理费用(年平均污水处理费用=
年的年平均污水处理费用(年平均污水处理费用= )
)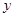 万元;
万元;
⑵为使该企业的年平均污水处理费用最低,问几年后需要重新更换新的污水处理设备?
已知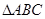 ,内角
,内角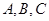 所对的边分别为
所对的边分别为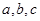 ,且满足下列三个条件:①
,且满足下列三个条件:①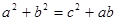 ②
②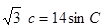 ③
③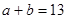
求 (1) 内角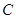 和边长
和边长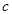 的大小;
的大小;
(2) 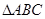 的面积.
的面积.