若函数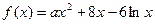 在点
在点 处的切线方程为
处的切线方程为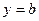
(1) 求 的值;
的值;
(2) 求 的单调递增区间;
的单调递增区间;
(3)若对于任意的 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围
的取值范围
(本小题满分12分)
已知向量 ,
,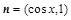 ,设函数
,设函数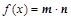 ,
, .
.
(Ⅰ)求函数 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(Ⅱ)若方程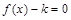 在区间
在区间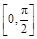 上有实数根,求
上有实数根,求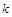 的取值范围.
的取值范围.
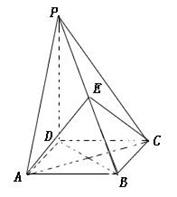
(本小题满分14分)如图,在三棱锥 中,面
中,面 面
面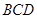 ,
,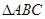 是正三角形,
是正三角形, 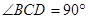 ,
, .
.
(Ⅰ)求证: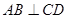 ;
;
(Ⅱ)求平面DAB与平面ABC的夹角的余弦值;
(Ⅲ)求异面直线 与
与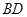 所成角的余弦值.
所成角的余弦值.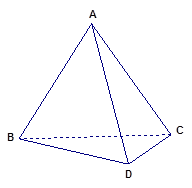
(本小题满分13分)把一个正方体的表面涂上红色,在它的长、宽、高上等距离地各切三刀,则大正方体被分割成64个大小相等的小正方体,将这些小正方体均匀地搅混在一起,如果从中任取1个,求下列事件的概率
(1)事件A=“这个小正方体各个面都没有涂红色”
(2)事件B=“这个小正方体只有1个面涂红色”
(3)事件C=“这个小正方体至少2个面涂红色”
(本小题满分12分)
已知p:方程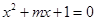 有两个不等的负根;
有两个不等的负根;
q:方程 无实根.若“p或q”为真,“p且q”为假,
无实根.若“p或q”为真,“p且q”为假,
求m的取值范围.
(本小题满分12分)四棱锥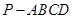 的底面是正方形,
的底面是正方形,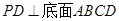 ,点E在棱PB上.若AB=
,点E在棱PB上.若AB=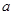 ,
,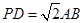
(Ⅰ)求证:平面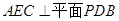 ;
;
(Ⅱ)若E为PB的中点时,求AE与平面PDB所成的角的大小.