(本小题满分12分)
已知向量 ,
,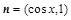 ,设函数
,设函数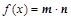 ,
, .
.
(Ⅰ)求函数 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(Ⅱ)若方程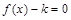 在区间
在区间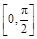 上有实数根,求
上有实数根,求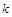 的取值范围.
的取值范围.
已知椭圆E的中心在坐标原点O,两个焦点分别为A(﹣1,0),B(1,0),一个顶点为H(2,0).
(1)求椭圆E的标准方程;
(2)对于x轴上的点P(t,0),椭圆E上存在点M,使得MP⊥MH,求实数t的取值范围.
已知椭圆的长轴长是短轴长的2倍,且过点A(2,﹣6)求椭圆的标准方程和离心率.
求椭圆 +y2=1的长轴和短轴的长、离心率、焦点和顶点的坐标.
+y2=1的长轴和短轴的长、离心率、焦点和顶点的坐标.
已知命题p:x1和x2是方程x2﹣mx﹣2=0的两个实根,不等式a2﹣5a﹣3≥|x1﹣x2|对任意实数m∈[﹣1,1]恒成立;命题q:不等式ax2+2x﹣1>0有解,若命题p是真命题,命题q是假命题,求a的取值范围.
已知命题p:1∈{x|x2<a};q:2∈{x|x2<a}
(1)若“p∨q”为真命题,求实数a的取值范围;
(2)若“p∧q”为真命题,求实数a的取值范围.