(本小题满分13分)把一个正方体的表面涂上红色,在它的长、宽、高上等距离地各切三刀,则大正方体被分割成64个大小相等的小正方体,将这些小正方体均匀地搅混在一起,如果从中任取1个,求下列事件的概率
(1)事件A=“这个小正方体各个面都没有涂红色”
(2)事件B=“这个小正方体只有1个面涂红色”
(3)事件C=“这个小正方体至少2个面涂红色”
(本小题满分14分)2014年8月以“分享青春,共筑未来”为口号的青奥会在江苏南京举行,
为此某商店经销一种青奥会纪念徽章,每枚徽章的成本为30元,并且每卖出一枚徽章需向相关部门上缴 元(
元( 为常数,
为常数, ),设每枚徽章的售价为
),设每枚徽章的售价为 元(35
元(35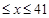 ).根据市场调查,日销售量与
).根据市场调查,日销售量与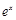 (
(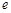 为自然对数的底数)成反比例.已知当每枚徽章的售价为40元时,日销售量为10枚.
为自然对数的底数)成反比例.已知当每枚徽章的售价为40元时,日销售量为10枚.
(1)求该商店的日利润 与每枚徽章的售价
与每枚徽章的售价 的函数关系式;
的函数关系式;
(2)当每枚徽章的售价为多少元时,该商店的日利润 最大?并求出
最大?并求出 的最大值.
的最大值.
(本小题满分14分)在四棱锥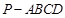 中,
中,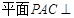 平面
平面 ,
,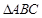 是边长为4的正三角形,
是边长为4的正三角形,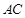 与
与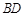 的交点
的交点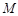 恰好是
恰好是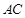 中点,又
中点,又 ,点
,点 在线段
在线段 上,且
上,且 .
.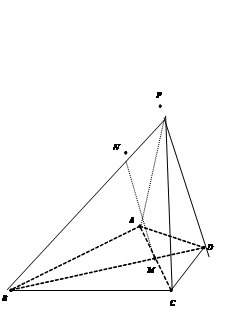
(1)求证: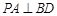 ;
;
(2)求证: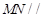 平面
平面 .
.
(本小题满分14分)如图,在 平面上,点
平面上,点 ,点
,点 在单位圆上,
在单位圆上, (
( )
)
(1)若点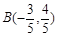 ,求
,求 的值;
的值;
(2)若 ,
,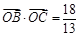 ,求
,求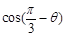 .
.
(本小题满分10分)设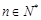 且
且 ,集合
,集合 的所有
的所有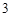 个元素的子集记为
个元素的子集记为 .
.
(1)求集合 中所有元素之和
中所有元素之和 ;
;
(2)记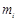 为
为
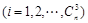 中最小元素与最大元素之和,求
中最小元素与最大元素之和,求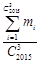 的值.
的值.
(选修4-5:不等式选讲)
设正数 满足
满足 ,求
,求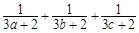 的最小值.
的最小值.