(选修4-5:不等式选讲)
设正数 满足
满足 ,求
,求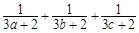 的最小值.
的最小值.
定义:对于函数 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足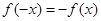 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数 ,试判断
,试判断 是否为定义域
是否为定义域 上的“局部奇函数”?若是,求出满足
上的“局部奇函数”?若是,求出满足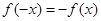 的
的 的值;若不是,请说明理由;
的值;若不是,请说明理由;
(2)若 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;
(3)若 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
已知:如图,等腰直角三角形 的直角边
的直角边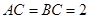 ,沿其中位线
,沿其中位线 将平面
将平面 折起,使平面
折起,使平面 ⊥平面
⊥平面 ,得到四棱锥
,得到四棱锥 ,设
,设 、
、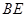 、
、 、
、 的中点分别为
的中点分别为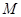 、
、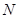 、
、 、
、 .
.


(1)求证: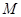 、
、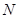 、
、 、
、 四点共面;
四点共面;
(2)求证:平面 平面
平面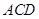 ;
;
(3)求异面直线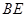 与
与 所成的角.
所成的角.
如图,已知圆 ,点
,点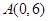 .
.
(1)求圆心在直线 上,经过点
上,经过点 ,且与圆
,且与圆 相外切的圆
相外切的圆 的方程;
的方程;
(2)若过点 的直线
的直线 与圆
与圆 交于
交于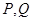 两点,且圆弧
两点,且圆弧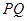 恰为圆
恰为圆 周长的
周长的 ,求直线
,求直线 的方程.
的方程.
如图,长方体 中,
中, ,点
,点 为
为 的中点.
的中点.
(1)求证:直线 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求 与平面
与平面 所成的角大小.
所成的角大小.
设全集为 ,集合
,集合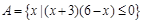 ,
,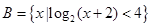 .
.
(1)求如图阴影部分表示的集合;
(2)已知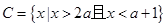 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.