（本题8分）甲、乙、丙三人独立完
成某项任务的概率分别为
。且他们是否完成任务互不影响。
（Ⅰ）若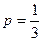
，设甲、乙、丙三人中能完成任务人数为X，求X的分布列和数学期望EX；
（Ⅱ）若三人中只有丙完成了任务的概率为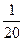
，求
的值
（本小题12分）
已知函数
是定义在
上的偶函数，当
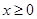时，
（1）求函数的解析式，并画出函数的图像。
（2）根据图像写出的单调区间和值域。
（本小题10分）
已知全集
,
、
、
，
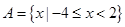求: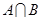 
; 
; 
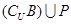(本小题满分12分)
已知Sn为数列{an}的前n项和，a1=9,Sn=n2an-n2(n-1),设bn=
(1)求证：bn-bn-1="n" (n≥2，n∈N).
(2)求
的最小值.
(本小题满分12分)
如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1,且AB⊥AC，M是CC1的中点，N是BC的中点，点P在直线A1B1上，且满足
(1)证明：PN⊥AM
(2)若
，求直线AA1与平面PMN所成角的正弦值.
(本小题满分12分)
设{an}是公差不为O的等差数列，Sn是其前n项和，已知
，且
(1)求数列{an}的通项an
(2)求等比数列{bn}满足b1=S1 ,b2=
, 求和Tn=a1b1+a2b2+…+anbn