(本小题满分12分)
已知Sn为数列{an}的前n项和,a1=9,Sn=n2an-n2(n-1),设bn=
(1)求证:bn-bn-1="n" (n≥2,n∈N).
(2)求 的最小值.
的最小值.
(本小题满分13分)已知动点P到定点 的距离和它到定直线
的距离和它到定直线 的距离的比值为
的距离的比值为 .
.
(Ⅰ)求动点P的轨迹W的方程;
(Ⅱ)若过点F的直线与点P的轨迹W相交于M,N两点(M,N均在y轴右侧),点 、
、 ,设A,B,M,N四点构成的四边形的面积为S,求S的取值范围.
,设A,B,M,N四点构成的四边形的面积为S,求S的取值范围.
(本小题满分12分)如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥底面ABC, ,∠A1AB=120°,D、E分别是BC、A1C1的中点.
,∠A1AB=120°,D、E分别是BC、A1C1的中点.
(Ⅰ)试在棱AB上找一点F,使DE∥平面A1CF;
(Ⅱ)在(Ⅰ)的条件下,求多面体BCF-A1B1C1的体积.
(本小题满分12分)已知数列{an},{bn}满足:a1b1+a2b2+a3b3+…+anbn= (
( ).
).
(Ⅰ)若{bn }是首项为1,公比为2等比数列,求数列{an}的通项公式;
(Ⅱ)在数列{an}中,a1=1,对任意 ,
, ,记数列{an+bn}的前n项和为Tn,求满足不等式
,记数列{an+bn}的前n项和为Tn,求满足不等式 的自然数n的最小值.
的自然数n的最小值.
(本小题满分12分)已知向量 ,
, ,函数
,函数 .
.
(Ⅰ)求 在区间
在区间 上的零点;
上的零点;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,  ,
, ,△ABC的面积
,△ABC的面积 ,求
,求 的值.
的值.
(本小题满分12分)
某校学生会进行了一次关于“消防安全”的调查活动,组织部分学生干部在几个大型小区随机抽取了50名居民进行问卷调查.活动结束后,团委会对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如下表:
| 年龄(岁) |
[10,20) |
[20,30) |
[30,40) |
[40,50) |
[50,60) |
[60,70] |
| 频数 |
m |
n |
14 |
12 |
8 |
6 |
| 知道的人数 |
3 |
4 |
8 |
7 |
3 |
2 |
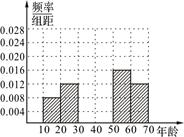
(Ⅰ)求上表中的m、n的值,并补全右图所示的的频率直方图;
(Ⅱ)在被调查的居民中,若从年龄在[10,20),[20,30)的居民中各随机选取1人参加消防知识讲座,求选中的两人中仅有一人不知道灭火器的使用方法的概率.