(本小题满分12分)
某校学生会进行了一次关于“消防安全”的调查活动,组织部分学生干部在几个大型小区随机抽取了50名居民进行问卷调查.活动结束后,团委会对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如下表:
| 年龄(岁) |
[10,20) |
[20,30) |
[30,40) |
[40,50) |
[50,60) |
[60,70] |
| 频数 |
m |
n |
14 |
12 |
8 |
6 |
| 知道的人数 |
3 |
4 |
8 |
7 |
3 |
2 |
(Ⅰ)求上表中的m、n的值,并补全右图所示的的频率直方图;
(Ⅱ)在被调查的居民中,若从年龄在[10,20),[20,30)的居民中各随机选取1人参加消防知识讲座,求选中的两人中仅有一人不知道灭火器的使用方法的概率.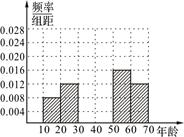
如图,建立平面直角坐标系
,
轴在地平面上,
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程
表示的曲线上,其中 与发射方向有关.炮的射程是指炮弹落地点的横坐标.
与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标
不超过多少时,炮弹可以击中它?请说明理由.
如图,在直三棱柱 中, , 分别是棱 上的点(点 不同于点 ),且 为 的中点.
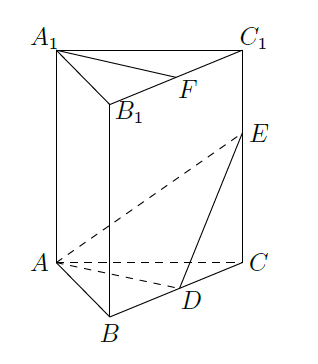
求证:(1)平面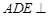 平面
平面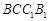 ;
;
(2)直线
平面
.
在
中,已知
.
(1)求证:
;
(2)若
,求
的值.
在
中,内角
的对边分别为
.已知
,
.
(1)求
的值;
(2)若
,求
的面积.
已知
,函数
.
(Ⅰ)证明:当
时,
(ⅰ)函数
的最大值为
;
(ⅱ)
;
(Ⅱ) 若
对
[0,1]恒成立,求
的取值范围.