已知函数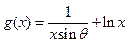 在
在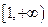 上为增函数,且
上为增函数,且 ,
,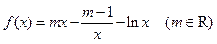 .
.
(Ⅰ)求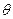 的值;
的值;
(Ⅱ)若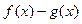 在
在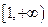 上为单调函数,求
上为单调函数,求 的取值范围;
的取值范围;
(Ⅲ)设 ,若
,若 在
在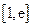 上至少存在一个
上至少存在一个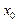 ,使得
,使得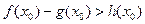 成立,求
成立,求 的取值范围.
的取值范围.
(本小题满分12分)已知函数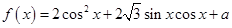 ,且当
,且当 时,
时, 的最小值为2,
的最小值为2,
(1)求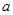 的值,并求
的值,并求 的单调递增区间;
的单调递增区间;
(2)先将函数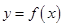 的图象上的点纵坐标不变,横坐标缩小到原来的
的图象上的点纵坐标不变,横坐标缩小到原来的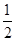 ,再将所得的图象向右平移
,再将所得的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求方程
的图象,求方程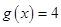 在区间
在区间 上所有根之和.
上所有根之和.
(本小题满分14分)已知焦点在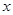 轴上的椭圆
轴上的椭圆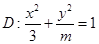 的离心率为
的离心率为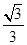 ,
,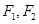 分别为左右焦点,过点
分别为左右焦点,过点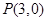 作直线交椭圆
作直线交椭圆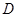 于
于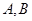 (
(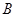 在
在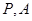 两点之间)两点,且
两点之间)两点,且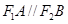 ,
,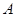 关于原点
关于原点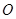 的对称点为
的对称点为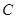 .
.
(1)求椭圆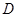 的方程;
的方程;
(2)求直线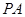 的方程;
的方程;
(3)过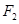 任作一直线交过
任作一直线交过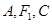 三点的圆于
三点的圆于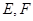 两点,求
两点,求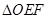 面积的取值范围.
面积的取值范围.
(本小题满分13分)已知函数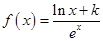 (其中
(其中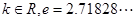 是自然对数的底数),
是自然对数的底数),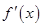 为
为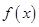 导函数。
导函数。
(1)当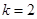 时,其曲线
时,其曲线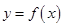 在点
在点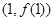 处的切线方程;
处的切线方程;
(2)若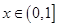 时,
时,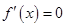 都有解,求
都有解,求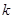 的取值范围;
的取值范围;
(3)若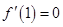 ,试证明:对任意
,试证明:对任意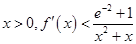 恒成立.
恒成立.
(本小题满分12分)数列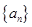 的前n项和为
的前n项和为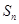 ,且
,且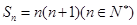
(1)求数列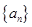 的通项公式;
的通项公式;
(2)若数列 满足:
满足: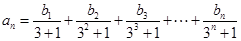 ,求数列
,求数列 的通项公式;
的通项公式;
(3)令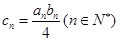 ,求数列
,求数列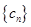 的 n项和
的 n项和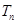 .
.
(本小题满分12分)已知一个袋子里装有只有颜色不同的6个小球,其中白球2个,黑球4个,现从中随机取球,每次只取一球.
(1)若每次取球后都放回袋中,求事件“连续取球四次,至少取得两次白球”的概率;
(2)若每次取球后都不放回袋中,且规定取完所有白球或取球次数达到五次就终止游戏,记游戏结束时一共取球X次,求随机变量X的分布列与期望.