已知椭圆 的两个焦点是
的两个焦点是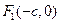 与
与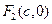
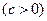 ,点
,点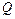 是椭圆外的动点,满足
是椭圆外的动点,满足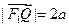 .点
.点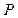 是线段
是线段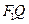 与该椭圆的交点,点
与该椭圆的交点,点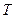 在线段
在线段 上,并且满足
上,并且满足 .
.
(Ⅰ)设 为点
为点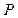 的横坐标,证明
的横坐标,证明 ;
;
(Ⅱ)求点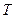 的轨迹
的轨迹 的方程;
的方程;
(Ⅲ)试问:在点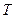 的轨迹
的轨迹 上,是否存在点
上,是否存在点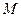 ,使
,使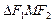 的面积为
的面积为 ?若存在,求
?若存在,求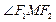 的正切值;若不存在,请说明理由.
的正切值;若不存在,请说明理由.
记等差数列{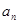 }的前n项和为
}的前n项和为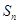 ,已知
,已知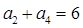 ,
,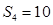 .
.
(Ⅰ)求数列{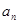 }的通项公式;
}的通项公式;
(Ⅱ)令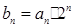
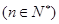 ,求数列{
,求数列{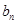 }的前项和
}的前项和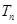 .
.
一种放射性元素,最初的质量为500g,按每年10﹪衰减.
(Ⅰ)求t年后,这种放射性元素质量ω的表达式;
(Ⅱ)由求出的函数表达式,求这种放射性元素的半衰期(剩留量为原来的一半所需要的时间).(精确到0.1;参考数据: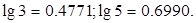 )
)
已知一条曲线上的点到定点 的距离是到定点
的距离是到定点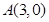 距离的二倍,求这条曲线的方程.
距离的二倍,求这条曲线的方程.
已知抛物线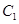 :
: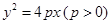 ,焦点为
,焦点为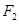 ,其准线与
,其准线与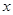 轴交于点
轴交于点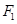 ;椭圆
;椭圆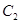 :分别以
:分别以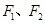 为左、右焦点,其离心率
为左、右焦点,其离心率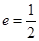 ;且抛物线
;且抛物线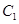 和椭圆
和椭圆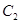
 的一个交点记为
的一个交点记为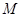 .
.
(1)当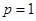 时,求椭圆
时,求椭圆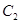 的标准方程;
的标准方程;
(2)在(1)的条件下,若直线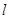 经过椭圆
经过椭圆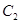 的右焦点
的右焦点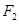 ,且
,且 与抛物线
与抛物线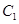 相交于
相交于 两点,若弦长
两点,若弦长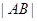 等于
等于 的周长,求直线
的周长,求直线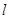 的方程
的方程 .
.
如图,三棱柱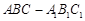 中,
中,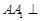 面
面 ,
,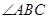 =
=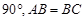 ,
,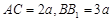 ,
,  为
为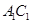 的中点,
的中点,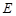 为
为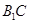 的中点:
的中点:
(1)求直线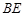 与
与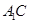 所成的角的余弦值;
所成的角的余弦值;
(2)在线段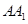 上是否存在点
上是否存在点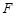 ,使
,使
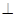 平面
平面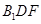 ,若存在,求出
,若存在,求出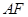 ;若不存在,说明理由。
;若不存在,说明理由。