在以 为原点的直角坐标系中,点
为原点的直角坐标系中,点 为
为 的直角顶点,若
的直角顶点,若 ,且点
,且点 的纵坐标大于0
的纵坐标大于0
(1)求向量 的坐标;
的坐标;
(2)是否存在实数 ,使得抛物线
,使得抛物线 上总有关于直线
上总有关于直线 对称的两个点?若存在,求实数
对称的两个点?若存在,求实数 的取值范围,若不存在,说明理由;
的取值范围,若不存在,说明理由;
已知函数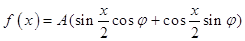
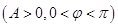 的最大值是2,且
的最大值是2,且 .
.
(1)求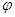 的值;
的值;
(2)已知锐角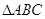 的三个内角分别为
的三个内角分别为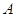 ,
, ,
,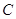 ,若
,若 ,求
,求 的值.
的值.
已知函数f(x)=x•lnx(e为无理数,e≈2.718)
(1)求函数f(x)在点(e,f(e))处的切线方程;
(2)设实数a> ,求函数f(x)在[a,2a]上的最小值;
,求函数f(x)在[a,2a]上的最小值;
(3)若k为正数,且f(x)>(k﹣1)x﹣k对任意x>1恒成立,求k的最大值.
已知椭圆C: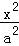 +
+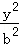 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是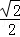 ,且点P(1,
,且点P(1,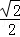 )在椭圆上.
)在椭圆上.
(1)求椭圆的方程;
(2)若过点D(0,2)的直线l与椭圆C交于不同的两点E,F,试求△OEF面积的取值范围(O为坐标原点).
已知四边形ABCD是矩形,AB=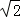 ,BC=
,BC= ,将△ABC沿着对角线AC折起来得到△AB1C,且顶点B1在平面AB=CD上射影O恰落在边AD上,如图所示.
,将△ABC沿着对角线AC折起来得到△AB1C,且顶点B1在平面AB=CD上射影O恰落在边AD上,如图所示.
(1)求证:AB1⊥平面B1CD;
(2)求三棱锥B1﹣ABC的体积VB1﹣ABC.
已知函数f(x)= sin
sin cos
cos ﹣cos2
﹣cos2 +
+
(1)若x∈[0,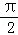 ],且f(x)=
],且f(x)=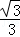 ,求cosx的值;
,求cosx的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足2bcosA≤2c+ a,求f(B)的取值范围.
a,求f(B)的取值范围.