在数列 中,已知a1=2,an+1=4an-3n+1,n∈
中,已知a1=2,an+1=4an-3n+1,n∈ .
.
(1)设 ,求数列
,求数列 的通项公式;
的通项公式;
(2)设数列 的前n项和为Sn,证明:对任意的n∈
的前n项和为Sn,证明:对任意的n∈ ,不等式Sn+1≤4Sn恒成立.
,不等式Sn+1≤4Sn恒成立.
设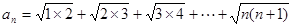 ,求证:
,求证: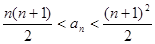
对于函数 与常数a,b,若
与常数a,b,若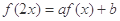 恒成立,则称(a,b)为函数
恒成立,则称(a,b)为函数 的一个“P数对”:设函数
的一个“P数对”:设函数 的定义域为
的定义域为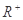 ,且f(1)=3.
,且f(1)=3.
(1)若(a,b)是 的一个“P数对”,且
的一个“P数对”,且 ,
, ,求常数a,b的值;
,求常数a,b的值;
(2)若(1,1)是 的一个“P数对”,求
的一个“P数对”,求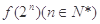 ;
;
(3)若(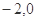 )是
)是 的一个“P数对”,且当
的一个“P数对”,且当 时,
时, ,求k的值及
,求k的值及 茌区间
茌区间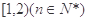 上的最大值与最小值.
上的最大值与最小值.
已知数列{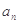 }的前n项和为
}的前n项和为 ,且满足
,且满足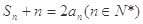 .
.
(1)证明:数列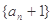 为等比数列,并求数列{
为等比数列,并求数列{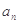 }的通项公式;
}的通项公式;
(2)数列{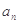 }满足
}满足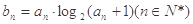 ,其前n项和为
,其前n项和为 ,试求满足
,试求满足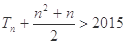 的最小正整数n.
的最小正整数n.
设函数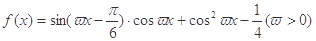 图像上的一个最高点为A,其相邻的一个最低点为B,且|AB|=
图像上的一个最高点为A,其相邻的一个最低点为B,且|AB|=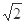 .
.
(1)求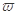 的值;
的值;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,且b+c=2,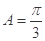 ,求
,求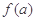
的值域.
已知函数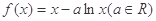
(1)当a=2时,求曲线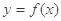 在点A(1,f(1))处的切线方程;
在点A(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性与极值.