(本小题满分10分)选修4-1:几何证明选讲
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
(1)求证: ;
;
(2)若 ,试求
,试求 的大小.
的大小.
已知函数f(x)=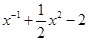 ,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
已知 若
若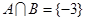 ,求实数
,求实数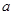 的值.
的值.
已知函数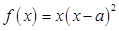 ,
,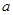 是大于零的常数.
是大于零的常数.
(Ⅰ)当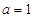 时,求
时,求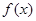 的极值;
的极值;
(Ⅱ)若函数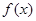 在区间
在区间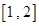 上为单调递增,求实数
上为单调递增,求实数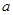 的取值范围;
的取值范围;
(Ⅲ)证明:曲线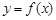 上存在一点
上存在一点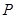 ,使得曲线
,使得曲线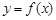 上总有两点
上总有两点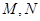 ,且
,且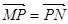 成立.
成立.
岛A观察站发现在其东南方向有一艘可疑船只,正以每小时10海里的速度向东南方向航行,观察站即刻通知在岛A正南方向B处巡航的海监船前往检查.接到通知后,海监船测得可疑船只在其北偏东75°方向且相距10海里的C处,随即以每小时10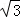 海里的速度前往拦截.
海里的速度前往拦截.
(I)问:海监船接到通知时,距离岛A多少海里?
(II)假设海监船在D处恰好追上可疑船只,求它的航行方向及其航行的时间.
设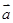 =(2cos
=(2cos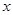 ,1),
,1),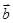 =(cos
=(cos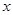 ,
,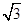 sin2
sin2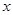 ),
),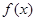 =
=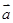 ·
·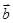 ,
,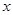
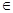 R.
R.
⑴若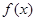 =0且
=0且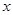
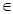 [
[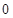 ,
,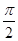 ],求
],求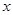 的值;
的值;
⑵若函数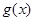 =
=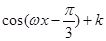 (
(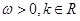 )与
)与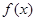 的最小正周期相同,且
的最小正周期相同,且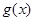 的图象过点(
的图象过点(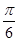 ,2),求函数
,2),求函数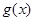 的值域及单调递增区间.
的值域及单调递增区间.