已知定义在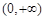 上的三个函数
上的三个函数 ,
, ,
,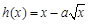 ,且
,且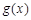 在
在 处取得极值.
处取得极值.


(1)求a的值及函数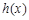 的单调区间.
的单调区间.
(2)求证:当 时,恒有
时,恒有 成立.[来源
成立.[来源
已知函数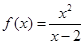 (x∈R,且x≠2).
(x∈R,且x≠2).
(1)求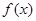 的单调区间;
的单调区间;
(2)若函数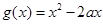 与函数
与函数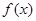 在x∈[0,1]上有相同的值域,求a的值.
在x∈[0,1]上有相同的值域,求a的值.
已知函数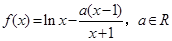 .
.
(1)若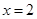 是函数
是函数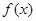 的极值点,求曲线
的极值点,求曲线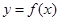 在点
在点 处的切线方程;
处的切线方程;
(2)若函数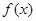 在
在 上为单调增函数,求
上为单调增函数,求 的取值范围.
的取值范围.
已知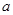 为实数,
为实数, .
.
(1)若 ,求
,求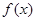 在
在 上的最大值和最小值;
上的最大值和最小值;
(2)若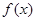 在
在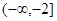 和
和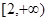 上都是递增的,求
上都是递增的,求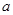 的取值范围.
的取值范围.
直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的方程为
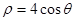 ,直线
,直线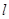 方程为
方程为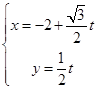 (t为参数),直线
(t为参数),直线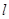 与C的公共点为T.
与C的公共点为T.
(1)求点T的极坐标;
(2)过点T作直线 ,
, 被曲线C截得的线段长为2,求直线
被曲线C截得的线段长为2,求直线 的极坐标方程.
的极坐标方程.