（本小题满分14分）
已知函数
，
，它们的定义域都是
，其中
，
（Ⅰ）当
时，求函数
的单调区间；
（Ⅱ）当时，对任意
，求证：
（Ⅲ）令
，问是否存在实数
使得
的最小值是3，如果存在，求出的值；如果不存在，说明理由。
某租赁公司拥有汽车100辆．当每辆车的月租金为3 000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．
(1)当每辆车的月租金定为3 600元时，能租出多少辆车？
(2)当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？
设函数f（x）=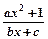
是奇函数（a,b,c都是整数）且f（1）=2,f（2）<3
（1）求a,b,c的值；
（2）当x<0，f（x）的单调性如何？用单调性定义证明你的结论。
已知f(x)＝x2－2x＋1，g(x)是一次函数，且f[g(x)]＝4x2，求g(x)的解析式．
提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情
况下，大桥上的车流速度v(单位：千米/小时)是车流密度x(单位：辆/千米)的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：
当20≤x≤200时，车流速度v是车流密度x的一次函数．当0≤x≤200时，求函数v(x)的表达式.
袋中有
个白球和
个黑球，每次从中任取个球，每次取出黑球后不再放回去，直到取出白球为止.求取球次数
的分布列，并求
出的期望值和方差.