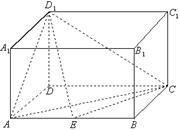
如图,在长方体 中,
中, 点
点 在棱
在棱 上移动.
上移动.
 (1)证明:
(1)证明: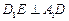 ;
;
(2)若 为
为 中点,求
中点,求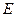 到面
到面 的距离;
的距离;
(3)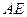 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为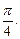
设函数
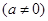 为奇函数,其图象在点
为奇函数,其图象在点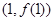 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数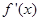 的最小值为
的最小值为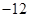 .
.
(Ⅰ)求 ,
, ,
,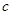 的值;
的值;
(Ⅱ)求函数 的单调递增区间,并求函数
的单调递增区间,并求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
如图,在四棱椎P-ABCD中,底面ABCD是边长为 的正方形,且PD=
的正方形,且PD= ,PA=PC=
,PA=PC= .
.
(1)求证:直线PD⊥面ABCD;
(2)求二面角A-PB-D的大小.
某生物学习小组对 、
、 两种珍惜植物种子的发芽率进行实验性实验,每实验一次均种下一粒
两种珍惜植物种子的发芽率进行实验性实验,每实验一次均种下一粒 种子和一粒
种子和一粒 种子.已知
种子.已知 、
、 两种种子在一定条件下每粒发芽的概率分别为
两种种子在一定条件下每粒发芽的概率分别为 .假设任何两粒种子是否发芽相互之间没有影响.
.假设任何两粒种子是否发芽相互之间没有影响.
(Ⅰ)求3粒 种子,至少有1粒未发芽的概率;
种子,至少有1粒未发芽的概率;
(Ⅱ)求 、
、 各3粒种子,
各3粒种子, 至少2粒发芽且
至少2粒发芽且 全发芽的概率.
全发芽的概率.
求函数 的单调递增区间.
的单调递增区间.
(10分)设 和
和 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量 表示方程
表示方程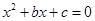 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(Ⅰ)求方程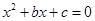 有实根的概率;
有实根的概率;
(Ⅱ)求 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程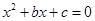 有实根的概率.
有实根的概率.