(本小题满分14分)
如图所示,已知曲线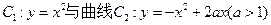 交于点O、A,直线
交于点O、A,直线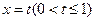 与曲线
与曲线 、
、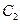 分别交于点D、B,连结OD,DA,AB.
分别交于点D、B,连结OD,DA,AB.
(1)求证:曲边四边形ABOD(阴影部分:OB为抛物线弧)的面积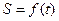 的函数表达式为
的函数表达式为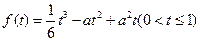

(2)求函数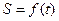 在区间
在区间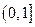 上的最大值.
上的最大值.
如图,在平面直角坐标系 中,平行于
中,平行于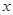 轴且过点
轴且过点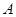 (3
(3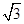 ,2)的入射光线
,2)的入射光线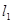 被直线
被直线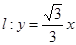 反射.反射光线
反射.反射光线 交
交 轴于
轴于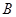 点,圆
点,圆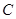 过点
过点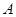 且与
且与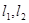 都相切。
都相切。
(1)求 所在直线的方程和圆
所在直线的方程和圆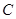 的方程;
的方程;
(2)设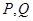 分别是直线
分别是直线 和圆
和圆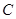 上的动点,求
上的动点,求 的最小值及此时点
的最小值及此时点 的坐标.
的坐标.
在正三棱锥 中,
中, 、
、 分别为棱
分别为棱 、
、 的中点,且
的中点,且 。
。
(1)求证:直线 平面
平面 ;
;
(2)求证:平面 平面
平面 。
。
如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点, ,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示。
,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示。
(Ⅰ)求出该几何体的体积;
(Ⅱ)试问在边 上是否存在点N,使
上是否存在点N,使 平面
平面 ? 若存在,确定点N的位置(不需证明);若不存在,请说明理由。
? 若存在,确定点N的位置(不需证明);若不存在,请说明理由。
已知命题 和命题
和命题 ,若
,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。
选修4-5:不等式选讲
已知函数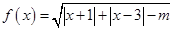 的定义域为
的定义域为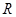 .
.
(1)求实数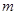 的取值范围;
的取值范围;
(2)若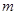 的最大值为
的最大值为 ,当正数
,当正数 满足
满足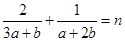 时,求
时,求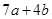 的最小值.
的最小值.