为了更好地服务于2010年世博会，上海某酒店随机地对最近入住的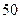
名旅客进行服务质量问卷调查，把旅客对住宿的舒适满意度与价格满意度分为五个等级：
“1级（很不满意）”、“2级（不满意）”、“3级（一般）”、“4级（满意）”、“5级（很满意）”其结果如表所示，若在这个样本中，任选一人，其舒适度为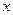
，价格满意度
.
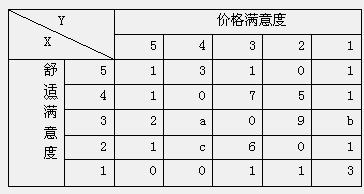
(1)根据样本中的数据求P（y=5）及P（x≥3且y=3）的值；
(2)若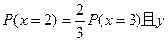
的期望值为
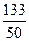，求a、b、c的值；
(3)求该人在对价格满意（满意度不低于3）的条件下对舒适度也满意的概率.
已知函数
．
（Ⅰ）当
时，求曲线
在原点处的切线方程；
（Ⅱ）当
时，讨论函数
在区间
上的单调性；
（Ⅲ）证明不等式
对任意
成立．
已知
，曲线
上任意一点
分别与点
、
连线的斜率的乘积为
．
（Ⅰ）求曲线的方程；
（Ⅱ）设直线
与
轴、
轴分别交于
、
两点，若曲线与直线
没有公共点，求证：
．
如图，已知多面体
的底面
是边长为
的正方形，
底面，
，且
．
（Ⅰ）求多面体的体积；
（Ⅱ）求直线
与平面
所成角的正弦值；
（Ⅲ）记线段BC的中点为K，在平面ABCD内过点K作一条直线与平面平行，要求保留作图痕迹，但不要求证明．
已知不等式2｜x－3｜＋｜x－4｜＜2a．
（Ⅰ）若a＝1，求不等式的解集；
（Ⅱ）若已知不等式的解集不是空集，求a的取值范围．
已知曲线C1的极坐标方程为ρcos（θ－
）＝－1，曲线C2的极坐标方程为ρ＝2
cos（θ－
）．以极点为坐标原点，极轴为x轴正半轴建立平面直角坐标系．
（Ⅰ）求曲线C2的直角坐标方程；
（Ⅱ）求曲线C2上的动点M到曲线C1的距离的最大值．