如图,已知矩形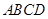 中,
中,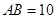 ,
, ,将矩形沿对角线
,将矩形沿对角线 把
把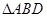 折起,使
折起,使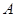 移到
移到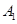 点,且
点,且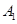 在平面
在平面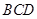 上的射影
上的射影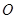 恰好在
恰好在 上.
上.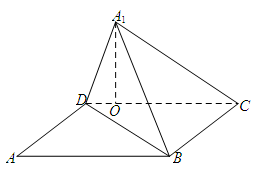
(1)求证: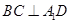 ;
;
(2)求证:平面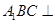 平面
平面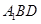 ;
;
(3)求二面角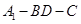 的余弦值.
的余弦值.
已知 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,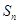 为
为 的前
的前 项和.
项和.
(Ⅰ)求通项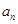 及
及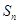 ;
;
(Ⅱ)设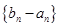 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列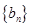 的通项公式及其前
的通项公式及其前 项和
项和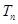 .
.
编号为 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 |
 |
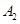 |
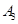 |
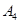 |
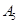 |
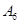 |
 |
 |
| 得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
| 运动员编号 |
 |
 |
 |
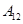 |
 |
 |
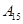 |
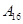 |
| 得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
| 区间 |
 |
 |
 |
| 人数 |
(Ⅱ)从得分在区间 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50的概率.
设 的导函数为
的导函数为 ,若函数
,若函数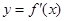 的图象关于直线
的图象关于直线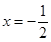 对称,且
对称,且 .
.
(Ⅰ)求实数 ,
,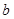 的值; (Ⅱ)求函数
的值; (Ⅱ)求函数 的极值。
的极值。
已知直线
(I)若以点
为圆心的圆与直线
相切与点
,且点
在
轴上,求该圆的方程;
(II)若直线
关于x轴对称的直线为
,问直线
与抛物线
是否相切?说明理由.
已知函数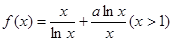 的图象经过
的图象经过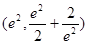
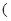 其中
其中 为自然对数的底数,
为自然对数的底数,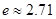
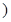 .
.
(Ⅰ)求实数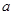 ;
;
(Ⅱ)求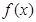 的单调区间;
的单调区间;
(Ⅲ)证明:对于任意的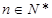 ,都有
,都有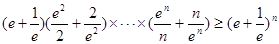 成立.
成立.