编号为 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 |
 |
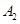 |
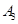 |
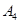 |
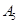 |
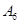 |
 |
 |
| 得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
| 运动员编号 |
 |
 |
 |
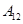 |
 |
 |
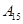 |
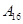 |
| 得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
| 区间 |
 |
 |
 |
| 人数 |
|
|
|
(Ⅱ)从得分在区间 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50的概率.
已知数列{an},a1=2a+1(a≠-1的常数),an=2an-1+n2-4n+2(n≥2,n∈N∗),数列{bn}的首项, b1=a,bn=an+n2(n≥2,n∈N∗).
(1)证明:{bn}从第2项起是以2为公比的等比数列并求{bn}通项公式;
(2)设Sn为数列{bn}的前n项和,且{Sn}是等比数列,求实数a的值;(3)当a>0时,求数列{an}的最小项.
已知函数f(x)= x/4+ln(x-2)/(x-4),(1)求函数f)x)的定义域和极值;(2)若函数(fx)在区间[a2-5a,8-3a]上为增函数,求实数a的取值范围;(3)函数f(x)的图象是否为中心对称图形?若是请指出对称中心,并证明;若不是,请说明理由.
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,点B的坐标为(2,0),(1)若动点M满足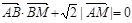 ,求点M的轨迹C;(2)若过点B的直线l′(斜率不等于零)与(1)中的轨迹C交于不同的两点E,F(E在B,F之间)试求△OBE与△OBF面积之比的取值范围.
,求点M的轨迹C;(2)若过点B的直线l′(斜率不等于零)与(1)中的轨迹C交于不同的两点E,F(E在B,F之间)试求△OBE与△OBF面积之比的取值范围.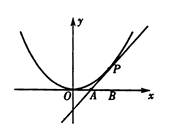
如图,已知矩形ABCD,PA⊥平面ABCD于A,M,N分别为AB,PC的中点
(1)求证:MN⊥AB;
(2)若平面PDC与平面ABCD所成的二面角为θ,能否确定θ,使直线MN是异面直线AB与PC的公垂线?若能确定,求出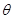 的值;若不能确定,说明理由.
的值;若不能确定,说明理由.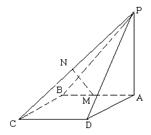
某工厂在试验阶段大量生产一种零件.这种零件有A,B两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为5/12,至少一项技术指标达标的概率为11/12.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率是多少?
(2)任意依次抽出5个零件进行检测,求其中至多3个零件是合格品的概率是多少?
(3)任意依次抽取该种零件4个,设ξ表示其中合格品的个数,求Eξ与Dξ.