在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为优秀,
分为优秀, 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的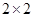 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为 .
.
| |
优秀 |
非优秀 |
合计 |
| 甲班 |
 |
|
|
| 乙班 |
|
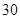 |
|
| 合计 |
|
|
 |
(1)请完成上面的列联表;
(2)根据列联表的数据,能否有 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?
(3)在甲、乙两个理科班优秀的学生中随机抽取两名学生,用 表示抽得甲班的学生人数,求
表示抽得甲班的学生人数,求 的分布列.
的分布列.
如图1,在直角梯形 中,
中,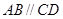 ,
,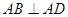 ,且
,且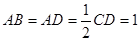 .
.
现以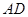 为一边向梯形外作正方形
为一边向梯形外作正方形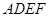 ,然后沿边
,然后沿边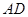 将正方形
将正方形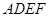 翻折,使平面
翻折,使平面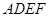 与平面
与平面 垂直,
垂直,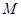 为
为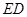 的中点,如图2.
的中点,如图2.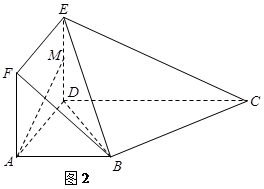
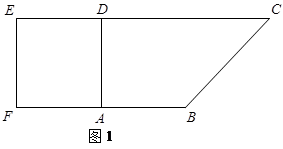
(1)求证: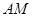 ∥平面
∥平面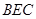 ;
;
(2)求证: ;
;
(3)求点 到平面
到平面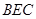 的距离.
的距离.
某校高三(1)班共有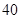 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在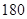 分钟到
分钟到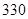 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计,得到如下频率分布表:
个组统计,得到如下频率分布表:
| 组别 |
分组 |
频数 |
频率 |
| 第一组 |
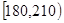 |
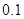 |
|
| 第二组 |
 |
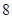 |
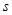 |
| 第三组 |
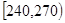 |
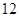 |
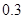 |
| 第四组 |
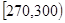 |
 |
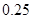 |
| 第五组 |
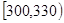 |
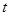 |
(1)求分布表中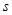 ,
,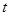 的值;
的值;
(2)王老师为完成一项研究,按学习时间用分层抽样的方法从这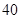 名学生中抽取
名学生中抽取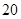 名进行研究,问应抽取多少名第一组的学生?
名进行研究,问应抽取多少名第一组的学生?
(3)已知第一组学生中男、女生人数相同,在(2)的条件下抽取的第一组学生中,既有男生又有女生的概率是多少?
已知函数
(1)求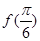 的值;
的值;
(2)若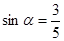 ,且
,且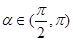 ,求
,求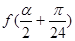 .
.
函数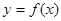 的定义域为
的定义域为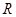 ,若存在常数
,若存在常数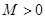 ,使得
,使得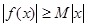 对一切实数
对一切实数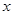 均成立,则称
均成立,则称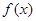 为“圆锥托底型”函数.
为“圆锥托底型”函数.
(1)判断函数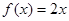 ,
,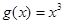 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.
(2)若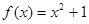 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出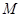 的最大值.
的最大值.
(3)问实数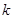 、
、 满足什么条件,
满足什么条件,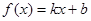 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.
我们将不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点称为切点.解决下列问题:
已知抛物线
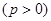 上的点
上的点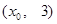 到焦点的距离等于4,直线
到焦点的距离等于4,直线 与抛物线相交于不同的两点
与抛物线相交于不同的两点 、
、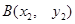 ,且
,且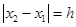 (
( 为定值).设线段
为定值).设线段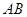 的中点为
的中点为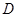 ,与直线
,与直线 平行的抛物线的切点为
平行的抛物线的切点为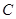 ..
..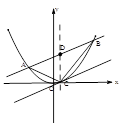
(1)求出抛物线方程,并写出焦点坐标、准线方程;
(2)用 、
、 表示出
表示出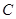 点、
点、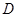 点的坐标,并证明
点的坐标,并证明 垂直于
垂直于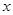 轴;
轴;
(3)求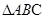 的面积,证明
的面积,证明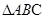 的面积与
的面积与 、
、 无关,只与
无关,只与 有关.
有关.