(本小题满分13分)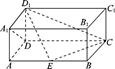
如图,在长方体 中,
中,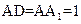 ,AB=2,点E在棱AB上移动.
,AB=2,点E在棱AB上移动.
(Ⅰ)证明: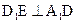 ;
;
(Ⅱ)当E为AB的中点时,求点A到面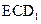 的距离;
的距离;
(Ⅲ)AE等于何值时,二面角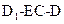 的大小为
的大小为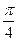 .
.
(本小题满分12分)
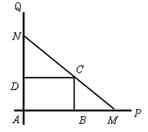
如下图,互相垂直的两条公路 、
、 旁有一矩形花园
旁有一矩形花园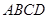 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园 ,要求点
,要求点 在射线
在射线 上,点
上,点 在射线
在射线 上,且直线
上,且直线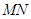 过点
过点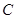 ,其中
,其中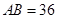 米,
米, 米. 记三角形花园
米. 记三角形花园 的面积为
的面积为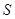 .
.
(Ⅰ)问: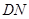 取何值时,
取何值时,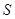 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(Ⅱ)若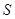 不超过1764平方米,求
不超过1764平方米,求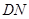 长的取值范围.
长的取值范围.
(本小题满分10分)
解关于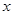 的不等式:
的不等式: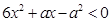 .
.
(本题12分)已知函数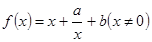 ,其中
,其中 .
.
(Ⅰ)若曲线 在点
在点 处的切线方程为
处的切线方程为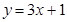 ,求函数
,求函数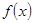 的解析式;
的解析式;
(Ⅱ)讨论函数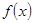 的单调性;
的单调性;
(Ⅲ)若对于任意的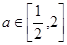 ,不等式
,不等式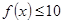 在
在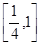 上恒成立,求
上恒成立,求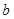 的取值范围.
的取值范围.
(本题10分)在直角坐标系xOy中,曲线C1的参数方程为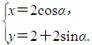 (α为参数)M是C1上的动点,P点满足
(α为参数)M是C1上的动点,P点满足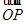 =2
=2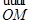 ,P点的轨迹为曲线C2.
,P点的轨迹为曲线C2.
(1)求C2的参数方程;
(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ= 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
(本题10分)已知函数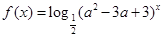
(1)判断函数的奇偶性
(2)若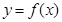 在
在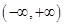 上为减函数,求
上为减函数,求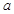 的取值范围。
的取值范围。