(本小题满分12分)已知数列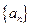 的前
的前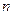 项和是
项和是 ,且
,且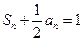 .
.
(Ⅰ)求数列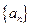 的通项公式;
的通项公式;
(Ⅱ)设
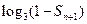 ,求适合方程
,求适合方程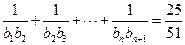 的
的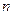 的值.
的值.
(Ⅲ)记 ,是否存在实数M,使得对一切
,是否存在实数M,使得对一切 恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
求与定点 及定直线
及定直线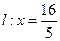 的距离的比是5:4的点P的轨迹
的距离的比是5:4的点P的轨迹
设F1、F2分别为椭圆C: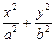 =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1, )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
已知圆C在x轴上的截距为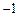 和3,在y轴上的一个截距为1.
和3,在y轴上的一个截距为1.
(1)求圆C的标准方程;
(2)若过点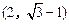 的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角.
的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角.
已知圆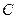 与两坐标轴都相切,圆心
与两坐标轴都相切,圆心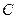 到直线
到直线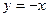 的距离等于
的距离等于 。
。
(1)求圆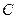 的方程。
的方程。
(2)若直线
 与圆
与圆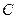 相切,求证
相切,求证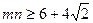 。
。
设F1、F2分别为椭圆C: =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1,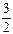 )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点P是(1)中所得椭圆上的动点,当P在何位置时, 最大,说明理由,并求出最大值。
最大,说明理由,并求出最大值。