如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.
(1)证明:BD⊥AA1;
(2)证明:平面AB1C//平面DA1C1
(3)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
已知以原点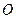 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为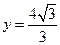 ,离心率
,离心率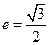 ,
,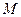 是椭圆上的动点。
是椭圆上的动点。
(Ⅰ)若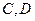 的坐标分别是
的坐标分别是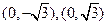 ,求
,求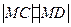 的最大值;
的最大值;
(Ⅱ)如题(20)图,点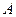 的坐标为
的坐标为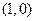 ,
,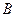 是圆
是圆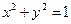 上的点,
上的点,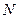 是点
是点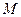 在
在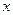 轴上的射影,点
轴上的射影,点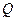 满足条件:
满足条件: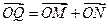 ,
,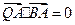 ,求线段
,求线段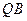 的中点
的中点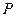 的轨迹方程。
的轨迹方程。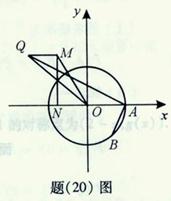
(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
如题(19)图,在四棱锥 中,
中,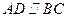 且
且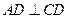 ;平面
;平面
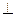 平面
平面 ,
, ;
; 为
为 的中点,
的中点,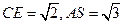 。求:
。求:
(Ⅰ)点 到平面
到平面 的距离;
的距离;
(Ⅱ)二面角 的大小。
的大小。
在直角坐标系中,△OAB的顶点坐标O(0 , 0),A(2, 0),B(1, ),求△OAB在矩阵MN的作用下变换所得到的图形的面积,其中矩阵 ,
,
如图,四边形ABCD内接于 ,
, ,过A点的切线交CB的延长线于E点.
,过A点的切线交CB的延长线于E点.
求证: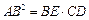 .
.
设方程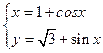 (q为参数)表示的曲线为C,求在曲线C上到原点O距离最小的点P的坐标.
(q为参数)表示的曲线为C,求在曲线C上到原点O距离最小的点P的坐标.