某投资公司2010年初准备将1000万投资到“低碳”项目上，现有两个项目可供选择
项目一：新能源汽车。据市场调研，投资到该项目上，到年底可获利30%，也可能亏损15%，且这两种情况发生的概率分别为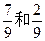
项目二：通信设备。据市场调研，投资到该项目上，到年底可获利50%，可能损失30%，也可能不赔不赚，且这三种情况发生的概率分别为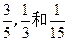
（1）针对以上两个投资项目，请你为投资公司选择一个合理的项目，并说明理由；
（2）若市场预期不变，该投资公司按照你选择的项目长期投资（每年的利润和本金继续用作投资），问大约在哪一年的年底该投资公司的总资产（利润+本金）可翻一番？（参考数据lg2=0.3010,lg3=0.4771）
（本
小题满分10分）选修4-5：不等式选讲
设函数
（I）若a=-1，解不等式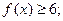
（II）如果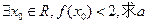
的取值范围。
请考生在22、23两题中任选一题作答，如果都做，则按所做的第一题记分。
（本小题满分10分）选修4-1：几何证明选讲
如图，AB是⊙O的直径，C、F为⊙O上的点，CA是∠BAF的角平分线，过点C
作CD⊥AF交AF的延长线于D点，CM⊥AB，垂足为点M。
（I）求证：DC是⊙O的切线； （II）求证：AM：MB=
DF·DA。
（本小题满分12分）
已知函数
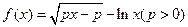是增函数。
（I）求实数p的取值范围；
（II）设数列
的通项公式为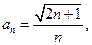
前n项和为S，求证：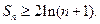
（本小题满分12分）
已知圆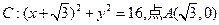
，Q是圆上一动点，AQ的垂直平分线交CQ于点M，设点M的轨迹为E。
（I）求轨迹E的方程；
（II）过点P（1，0）的直线
交轨迹E于两个不同的点A、B，
（O是坐标原点）的面积
，若弦AB的中点为R，求直线OR斜率的取值范围。
（本小题满分12分）
如图，正方形ADEF和等腰梯形ABCD垂直，已知BC=2AD=4，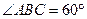
，
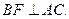
（I）求证：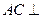
面ABF；
（II）求异面直线BE与AC所成的角的余弦值；
（III）在线段BE上是否存在一点P，使得平面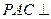
平面BCEF？若存在，求出
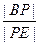的值，若不存在，请说明理由。