已知关于 的不等式:
的不等式:
(1)当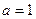 时,求该不等式的解集;(2)当
时,求该不等式的解集;(2)当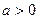 时,求该不等式的解集.
时,求该不等式的解集.
已知函数 。
。
(1)若函数 是
是 上的增函数,求实数
上的增函数,求实数 的取值范围;
的取值范围;
(2)当 时,若不等式
时,若不等式 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)对于函数 若存在区间
若存在区间 ,使
,使 时,函数
时,函数 的值域也是
的值域也是 ,则称
,则称 是
是 上的闭函数。若函数
上的闭函数。若函数 是某区间上的闭函数,试探求
是某区间上的闭函数,试探求 应满足的条件。
应满足的条件。
设函数 是定义在
是定义在 上的偶函数.若当
上的偶函数.若当 时,
时,

(1)求 在
在 上的解析式.
上的解析式.
(2)请你作出函数 的大致图像.
的大致图像.
(3)当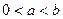 时,若
时,若 ,求
,求 的取值范围.
的取值范围.
(4)若关于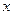 的方程
的方程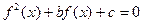 有7个不同实数解,求
有7个不同实数解,求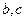 满足的条件.
满足的条件.
已知函数 .
.
(1)若 ,求
,求 的值;
的值;
(2)若 对于
对于 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知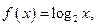 当点
当点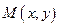 在
在 的图像上运动时,点
的图像上运动时,点 函数
函数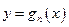 的图像上运动
的图像上运动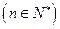 。
。
(1)求 的表达式;
的表达式;
(2)若集合 {
{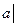 关于
关于 的方程
的方程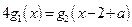 有实根,
有实根, },求集合A;
},求集合A;
(3)设 函数
函数 的定义域为
的定义域为 <
<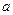
 值域为
值域为 ,求实数
,求实数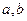 的值。
的值。