如图,已知四边形ABCD 是矩形,PA⊥平面ABCD,M, N分别是AB, PC的中点.
(1)求证:MN∥平面PAD;
(2)求证:MN⊥DC;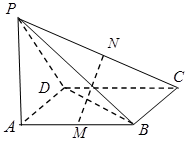
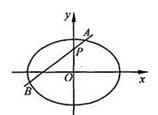
【2015高考四川,理20】如图,椭圆E: 的离心率是
的离心率是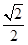 ,过点P(0,1)的动直线
,过点P(0,1)的动直线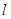 与椭圆相交于A,B两点,当直线
与椭圆相交于A,B两点,当直线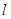 平行与
平行与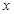 轴时,直线
轴时,直线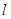 被椭圆E截得的线段长为
被椭圆E截得的线段长为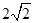 .
.
(1)求椭圆E的方程;
(2)在平面直角坐标系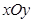 中,是否存在与点P不同的定点Q,使得
中,是否存在与点P不同的定点Q,使得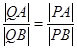 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
【2015高考重庆,理21】如图,椭圆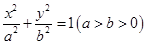 的左、右焦点分别为
的左、右焦点分别为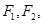 过
过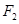 的直线交椭圆于
的直线交椭圆于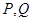 两点,且
两点,且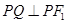

(1)若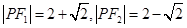 ,求椭圆的标准方程
,求椭圆的标准方程
(2)若 求椭圆的离心率
求椭圆的离心率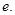
【2015高考天津,理19】(本小题满分14分)已知椭圆 的左焦点为
的左焦点为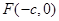 ,离心率为
,离心率为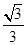 ,点M在椭圆上且位于第一象限,直线
,点M在椭圆上且位于第一象限,直线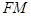 被圆
被圆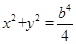 截得的线段的长为c,
截得的线段的长为c,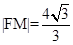 .
.
(Ⅰ)求直线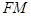 的斜率;
的斜率;
(Ⅱ)求椭圆的方程;
(Ⅲ)设动点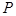 在椭圆上,若直线
在椭圆上,若直线 的斜率大于
的斜率大于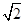 ,求直线
,求直线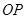 (
(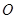 为原点)的斜率的取值范围.
为原点)的斜率的取值范围.
【2015高考安徽,理20】设椭圆E的方程为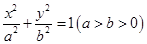 ,点O为坐标原点,点A的坐标为
,点O为坐标原点,点A的坐标为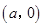 ,点B的坐标为
,点B的坐标为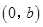 ,点M在线段AB上,满足
,点M在线段AB上,满足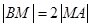 ,直线OM的斜率为
,直线OM的斜率为 .
.
(Ⅰ)求E的离心率e;
(Ⅱ)设点C的坐标为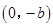 ,N为线段AC的中点,点N关于直线AB的对称点的纵坐标为
,N为线段AC的中点,点N关于直线AB的对称点的纵坐标为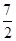 ,求E的方程.
,求E的方程.
【2015高考山东,理20】平面直角坐标系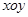 中,已知椭圆
中,已知椭圆 的离心率为
的离心率为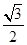 ,左、右焦点分别是
,左、右焦点分别是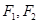 ,以
,以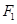 为圆心以3为半径的圆与以
为圆心以3为半径的圆与以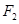 为圆心以1为半径的圆相交,且交点在椭圆
为圆心以1为半径的圆相交,且交点在椭圆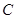 上.
上.
(Ⅰ)求椭圆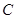 的方程;
的方程;
(Ⅱ)设椭圆 ,
,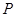 为椭圆
为椭圆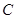 上任意一点,过点
上任意一点,过点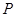 的直线
的直线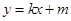 交椭圆
交椭圆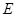 于
于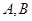 两点,射线
两点,射线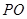 交椭圆
交椭圆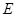 于点
于点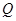 .
.
(ⅰ)求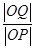 的值;
的值;
(ⅱ)求 面积的最大值.
面积的最大值.