(本题满分12分,第(1)小题6分,第(2)小题6分)
如图,在棱长为1的正方体中,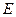 是棱
是棱 的中点,
的中点,
(1)求证: ;
;
(2)求 与平面
与平面 所成角大小(用反三角函数表示).
所成角大小(用反三角函数表示).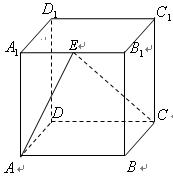
已知函数 (
( ,
, 为自然对数的底数).
为自然对数的底数).
(1)若曲线 在点
在点 处的切线平行于
处的切线平行于 轴,求
轴,求 的值;
的值;
(2)求函数 的极值;
的极值;
(3)当 的值时,若直线
的值时,若直线 与曲线
与曲线 没有公共点,求
没有公共点,求 的最大值.
的最大值.
(注:可能会用到的导数公式: ;
; )
)
已知椭圆C: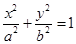 (
( )的短轴长为2,离心率为
)的短轴长为2,离心率为 .
.
(1)求椭圆C的方程
(2)若过点M(2,0)的引斜率为 的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足
的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足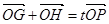 (O为坐标原点),当
(O为坐标原点),当 时,求实数
时,求实数 的取值范围?
的取值范围?
从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
| 分组(重量) |
 |
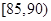 |
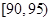 |
 |
| 频数(个) |
5 |
10 |
20 |
15 |
(1)根据频数分布表计算苹果的重量在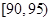 的频率;
的频率;
(2)用分层抽样的方法从重量在 和
和 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在 的有几个?
的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在 和
和 中各有1个的概率.
中各有1个的概率.
如图,三棱柱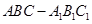 中,
中,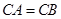 ,
, ,
,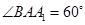 .
.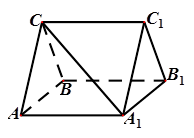
(1)证明: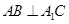 ;
;
(2)若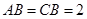 ,
,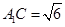 ,求三棱柱
,求三棱柱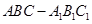 的体积.
的体积.
已知向量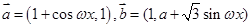 (
( 为常数且
为常数且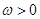 ),函数
),函数 在
在 上的最大值为
上的最大值为 .
.
(1)求实数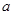 的值;
的值;
(2)把函数 的图象向右平移
的图象向右平移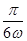 个单位,可得函数
个单位,可得函数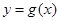 的图象,若
的图象,若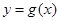 在
在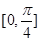 上为增函数,求
上为增函数,求 取最大值时的单调增区间.
取最大值时的单调增区间.