已知函数 (
( ,
, 为自然对数的底数).
为自然对数的底数).
(1)若曲线 在点
在点 处的切线平行于
处的切线平行于 轴,求
轴,求 的值;
的值;
(2)求函数 的极值;
的极值;
(3)当 的值时,若直线
的值时,若直线 与曲线
与曲线 没有公共点,求
没有公共点,求 的最大值.
的最大值.
(注:可能会用到的导数公式: ;
; )
)
(本小题满分14分)设函数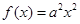 (
(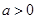 ),
),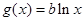 .
.
(Ⅰ)令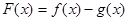 ,讨论
,讨论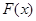 的单调性;
的单调性;
(Ⅱ)关于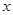 的不等式
的不等式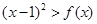 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数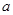 的取值范围;
的取值范围;
(Ⅲ)对于函数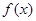 与
与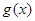 定义域上的任意实数
定义域上的任意实数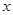 ,若存在常数
,若存在常数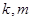 ,使得
,使得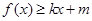 和
和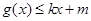 都成立,则称直线
都成立,则称直线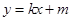 为函数
为函数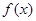 与
与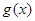 的“分界线”.设
的“分界线”.设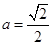 ,
,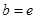 ,试探究
,试探究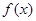 与
与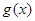 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
(本小题满分14分)广东某民营企业主要从事美国的某品牌运动鞋的加工生产,按国际惯例以美元为结算货币,依据以往加工生产的数据统计分析,若加工产品订单的金额为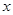 万美元,可获得加工费近似为
万美元,可获得加工费近似为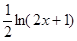 万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失
万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失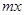 万美元,其中
万美元,其中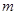 为该时段美元的贬值指数,
为该时段美元的贬值指数,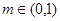 ,从而实际所得的加工费为
,从而实际所得的加工费为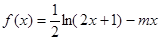 (万美元).
(万美元).
(Ⅰ)若某时期美元贬值指数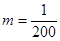 ,为确保企业实际所得加工费随
,为确保企业实际所得加工费随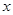 的增加而增加,该企业加工产品订单的金额
的增加而增加,该企业加工产品订单的金额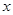 应在什么范围内?
应在什么范围内?
(Ⅱ)若该企业加工产品订单的金额为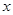 万美元时共需要的生产成本为
万美元时共需要的生产成本为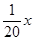 万美元,已知该企业加工生产能力为
万美元,已知该企业加工生产能力为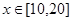 (其中
(其中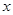 为产品订单的金额),试问美元的贬值指数
为产品订单的金额),试问美元的贬值指数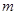 在何范围时,该企业加工生产将不会出现亏损.
在何范围时,该企业加工生产将不会出现亏损.
(本小题满分13分)函数
 的部分图象如下图所示,该图象与
的部分图象如下图所示,该图象与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,
, 为最高点,且
为最高点,且 的面积为
的面积为 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ) ,求
,求 的值.
的值.
(Ⅲ)将函数 的图象的所有点的横坐标缩短到原来的
的图象的所有点的横坐标缩短到原来的 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移 个单位,得函数
个单位,得函数 的图象,若函数
的图象,若函数 为奇函数,求
为奇函数,求 的最小值.
的最小值.
(本小题满分13分)已知向量 ,
, ,若
,若 .
.
(Ⅰ) 求函数 的最小正周期;
的最小正周期;
(Ⅱ) 已知 的三内角
的三内角 的对边分别为
的对边分别为 ,且
,且 ,
, (A为锐角),
(A为锐角), ,求
,求 的值.
的值.
设P:二次函数 在区间
在区间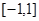 上存在零点;Q:函数
上存在零点;Q:函数 在
在 内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数
内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数 的取值范围.
的取值范围.