(本小题满分13分)函数
的部分图象如下图所示，该图象与
轴交于点
，与
轴交于点
，
为最高点，且
的面积为
．
（Ⅰ）求函数
的解析式；
（Ⅱ）
，求
的值．
（Ⅲ）将函数
的图象的所有点的横坐标缩短到原来的
倍（纵坐标不变），再向左平移
个单位，得函数
的图象，若函数为奇函数，求
的最小值.
如图,在四棱椎P－ABCD中,底面ABCD是边长为
的正方形,且PD=,PA=PC=
.
(1)求证:直线PD⊥面ABCD;
(2)求二面角A－PB－D的大小.
某生物学习小组对
、
两种珍惜植物种子的发芽率进行实验性实验，每实验一次均种下一粒种子和一粒种子.已知
、两种种子在一定条件下每粒发芽的概率分别为
.假设任何两粒种子是否发芽相互之间没有影响.
（Ⅰ）求3粒种子，至少有1粒未发芽的概率；
（Ⅱ）求、各3粒种子，至少2粒发芽且全发芽的概率.
求函数
的单调递增区间.
(10分)设
和
分别是先后抛掷一枚骰子得到的点数，用随机变量
表示方程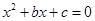
实根的个数（重根按一个计）．
（Ⅰ）求方程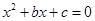有实根的概率；
（Ⅱ）求的分布列和数学期望；
（Ⅲ）求在先后两次出现的点数中有5的条件下，方程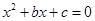有实根的概率.
(10分)某运动员射击一次所得环数
的分布如下：
|
0~6 |
7 |
8 |
9 |
10 |
 |
0 |
 |
 |
|
|
现进行两次射击，以该运动员两次射击中最高环数作为他的成绩，记为
.
(I)求该运动员两次都命中7环的概率
(II)求的分布列
(III)求的数学期望