(本题满分10分)某汽车运输公司购买了一批豪华大客车投入运营.据市场分析,每辆客车运营的总利润y(单位:十万元)与运营年数x满足二次函数的关系: ,且该二次函数图像过点(4,7).问每辆客车运营多少年,运营的年平均利润最大?最大值为多少?(年平均利润=
,且该二次函数图像过点(4,7).问每辆客车运营多少年,运营的年平均利润最大?最大值为多少?(年平均利润= )
)
(本题满分14分)已知抛物线 的焦点为F,点P是抛物线上的一点,且其纵坐标为4,
的焦点为F,点P是抛物线上的一点,且其纵坐标为4, .
.
(1)求抛物线的方程;
(2)设点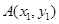 ,
,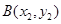 (
( )是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
)是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
(本小题满分14分)设数列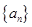 是公比为正数的等比数列,
是公比为正数的等比数列,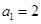 ,
, .
.
(1)求数列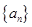 的通项公式;
的通项公式;
(2)若数列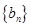 满足:
满足: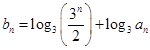 ,求数列
,求数列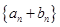 的前
的前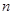 项和
项和 .
.
(本小题满分14分)如图,在三棱锥P- ABC中,已知平面PBC 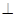 平面ABC.
平面ABC.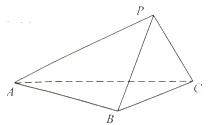
(1)若AB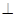 BC,CP
BC,CP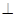 PB,求证:CP
PB,求证:CP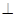 PA:
PA:
(2)若过点A作直线 ⊥平面ABC,求证:
⊥平面ABC,求证: //平面PBC.
//平面PBC.
【原创】设复数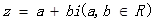 ,
,
(1)若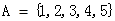 ,
, ,求复数
,求复数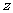 的实部为奇数,虚部为偶数的概率;
的实部为奇数,虚部为偶数的概率;
(2) 若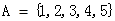 ,
, ,设
,设 表示直线
表示直线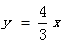 与圆
与圆 的交点个数,列出
的交点个数,列出 的概率分布列,并求出
的概率分布列,并求出 的数学期望;
的数学期望;
(本小题满分12分)已知向量 ,函数
,函数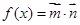 .
.
(1)求函数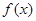 的单调递增区间;
的单调递增区间;
(2)在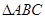 中,角
中,角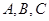 的对边分别为
的对边分别为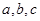 ,若
,若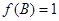 ,
,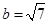 ,
,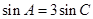 ,求
,求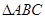 的面积.
的面积.