下表是某班英语和数学成绩的分布表,已知该班有50名学生,成绩分为1~5个档次。如:表中英语成绩是4分、数学成绩是2分的人数有5人。现设该班任意一位学生的英语成绩为m,数学成绩为n。
| n m |
数学 |
|||||
| 5 |
4 |
3 |
2 |
1 |
||
| 英 语 |
5 |
1 |
3 |
1 |
0 |
1 |
| 4 |
1 |
0 |
7 |
5 |
1 |
|
| 3 |
2 |
1 |
0 |
9 |
3 |
|
| 2 |
1 |
b |
6 |
0 |
a |
|
| 1 |
0 |
0 |
1 |
1 |
3 |
(1)求m=4,n=3的概率;
(2)求在m≥3的条件下,n=3的概率;
(3)求a+b的值,并求m的数学期望;
(4)若m=2与n=4是相互独立的,求a,b的值。
己知命题 :方程
:方程 表示焦点在
表示焦点在 轴的椭圆;命题
轴的椭圆;命题 :关于
:关于 的不等式
的不等式 的解集是R;若“
的解集是R;若“ ” 是假命题,“
” 是假命题,“ ”是真命题,求实数
”是真命题,求实数 的取值范围。
的取值范围。
在直角坐标系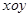 上取两个定点
上取两个定点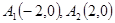 ,再取两个动点
,再取两个动点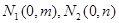 且
且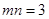 .
.
(I)求直线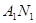 与
与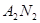 交点的轨迹
交点的轨迹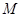 的方程;
的方程;
(II)已知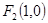 ,设直线:
,设直线: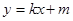 与(I)中的轨迹
与(I)中的轨迹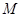 交于
交于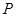 、
、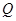 两点,直线
两点,直线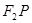 、
、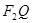 的倾斜角分别为
的倾斜角分别为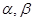 且
且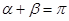 ,求证:直线过定点,并求该定点的坐标.
,求证:直线过定点,并求该定点的坐标.
如图,已知DE⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点。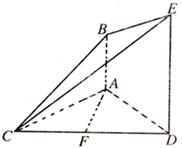
(I)求证:AF//平面BCE;
(II)求证:平面BCE⊥平面CDE;
(III)求平面BCE与平面ACD所成锐二面角的大小。
已知一个圆的圆心为坐标原点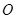 ,半径为
,半径为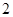 .从这个圆上任意一点
.从这个圆上任意一点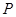 向
向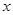 轴作垂线
轴作垂线 ,
,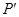 为垂足.
为垂足.
(Ⅰ)求线段 中点
中点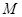 的轨迹方程;
的轨迹方程;
(Ⅱ)已知直线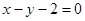 与
与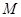 的轨迹相交于
的轨迹相交于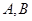 两点,求
两点,求 的面积
的面积
已知定点F(2,0)和定直线 ,动圆P过定点F与定直线相切,记动圆圆心P的轨迹为曲线C
,动圆P过定点F与定直线相切,记动圆圆心P的轨迹为曲线C
(1)求曲线C的方程.
(2)若以M(2,3)为圆心的圆与抛物线交于A、B不同两点,且线段AB是此圆的直径时,求直线AB的方程