如图,已知DE⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点。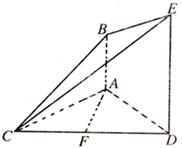
(I)求证:AF//平面BCE;
(II)求证:平面BCE⊥平面CDE;
(III)求平面BCE与平面ACD所成锐二面角的大小。
如图,四棱锥
中,
底面
,点
在线段
上,且
.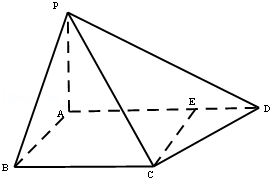
(Ⅰ)求证:
平面
;
(Ⅱ)若
,求四棱锥
的体积.
某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| 1 |
2 |
3 |
4 |
5 |
|
| 0.2 |
0.45 |
(Ⅰ)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求
、
、
的值;
(Ⅱ)在(Ⅰ)的条件下,将等级系数为4的3件日用品记为
,
,
,等级系数为5的2件日用品记为
,
,现从
,
,
,
,
这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
如图,直线
与抛物线
相切于点
.
(Ⅰ)求实数
的值;
(Ⅱ)求以点
为圆心,且与抛物线
的准线相切的圆的方程.

已知等差数列
中,
.
(Ⅰ)求数列
的通项公式;
(Ⅱ)若数列
的前
项和
,求
的值.
设实数数列
的前
项和
满足
.
(Ⅰ)若
成等比数列,求
.
(Ⅱ)求证:对
有
.